专题讲座三推广的余数定理及其算法

设F是一个数域，f (x)是F上的一个n次多项式（n≥1）. 对任何a∈F，(x – a)除f (x)的余式是一个数r，余数定理告诉我们r = f (a). 我们将从三个方面研究和解推广余数定理：

（Q1）：设是F上的m个互异的数(m≤n)，

如何计算除f (x)的余式?

(Q2)：如果再加一项与互异，令

那么(x)与之间有没有递推事例？

（Q3）：如果不一定互异，也就是如何计算

除f (x)的余式.

1 余式的计算问题

1．1  Lagrange插值法

设

是一个次数不超过m – 1的多项式且满足：

（1）

是唯一存在的.

是一个次数不超过m – 1且满足(1)的多项式.

1．2 待定系数法

设表示F [x]中次数不超过m – 1的多项式（包括零）全体，它是一个m维子空间，可以证明下列m个多项式

线性无关，因此存在唯一一组数使：

得出方程组

（2）

这个方程组的系数矩阵是下三角的，很容易求解，同时为找与之间的关系提供了帮助（我们将在§2中讨论这个问题），下面通过例子介绍方法2.

例1设，求

除f (x)的余式.

解设

于是得出方程

余式

使用方法二同样可以用解决f (x)除以

的余式计算问题.

例2设求

除f (x)的余式.

解应是一个次数不超过3的多项式：（3）

此时，可以证明：

是的基，可令：

由（3）式：，得到方程组如下：

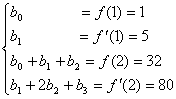
上述方程组仍是下三角的，它不仅易于求解，同样可以解决递推问题.

1．3 累次综合除法

下面通过一个例子介绍，其对一般情况的解决方法已包含在其中.

例3设

（1），求除f (x)的余式及商式

（2），求除f (x)的余式及商式.

解：（1）

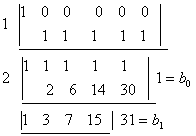
上式成立的原因在于：

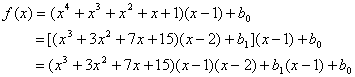
（2）

2 递推关系

设除f (x)的余式已经算出

再增加一个因子，相应的应是中的多项式，自然取的基为

得

代入上式，可以看出与都是（2）的解，因此，而由下面方程

确定，解出：

式中：

例4求设除的余式

解我们使用递推公式计算

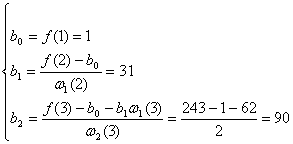
注：以上介绍的三种求的方法各有优点：方法1的形式最优美且便于计算机计算，方法2易于递推，方法3便于人工计算.