专题讲座七一类特殊矩阵的特征值

1  矩阵A=的特征值

定理1设，为n维向量，则A=的特征值为==…==0，=.

证由==

得

设为A的特征值，为A的对应于的特征向量

有，

从而

得= 0 即或

又

故==…==0，==.

例设向量0，，且，令，（1）求；（2）求A的特征值及特征向量.

解（1）

（2）由定理1知的特征值为：

==…==0，

易得A对应于特征值0的特征向量为

（不全为零）

其中，，……，.

2  的特征值

定理设，，…，为n阶复矩阵A的全部特征值，为复数域上次数大于零的多项式，则，，…，为的全部特征值.

推论1 设为n维列向量，为任意数，则的特征值为

==…==，.

证由定理1及定理2即得.

例设n阶矩阵

(1)求A的特征值和特征向量；

(2)求可逆矩阵，使为对角矩阵.

分析：注意到

其中

由推论1，易得A的特征值为

，.

再求A的特征向量及满足条件的可逆矩阵P(见[2]).

3   行列式的值

定理   A为n阶矩阵,为A的n个特征值,

则.

推论2   设为n维列向量,为任意数，则

证由命题3及推论1即得.

例已知齐次线性方程组

其中，试讨论和b满足何种关系时，

（1）方程组仅有零解；

（2）方程组有非零解？在有非零解时，求此方程组的一个基础解系.

分析：注意到方程组的系数矩阵为

令，

则

故

下面根据或讨论方程组解的情况（见[2]）.

例设齐次线性方程组

其中. 试讨论为何值时，方程组仅有零解；无穷多组解？在有无穷多组解时，求出全部解，并用基础解系表示全部解.

分析：注意到方程组的系数矩阵

.

令.  则

从而.

下面根据或讨论方程组解的情况（见[2]）.

例设，为实数，求证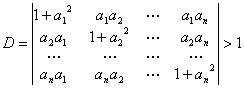

证注意到

其中

故.

例计算

解注意到

令，

则==.

参考文献

[1]王品超.高等代数新方法[M].山东：山东教育出版社，1989，77，81

[2]童武.全国硕士研究生入学考试历年试题精解（数学三）[M].北京：北京大学出版社，2004，7，10，12，24

[3]张禾瑞，郝炳新.高等代数（第四版）[M].北京：高等教育出版社，1999，294，298