专题讲座五行列式的计算方法
1.递推法
例1求行列式的值：
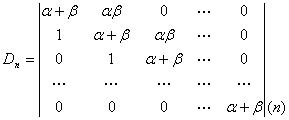（1）
的构造是：主对角线元全为
；主对角线上方第一条次对角线的元全为
，下方第一条次对角线的元全为1，其余元全为0；即为三对角线型。又右下角的（n）表示行列式为n阶。
解把类似于，但为k阶的三对角线型行列式记为
。
把（1）的行列式按第一列展开，有两项，一项是
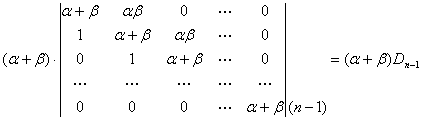
另一项是
上面的行列式再按第一行展开，得乘一个n – 2 阶行列式，这个n – 2 阶行列式和原行列式的构造相同，于是有递推关系：
（2）
移项，提取公因子β：
类似地：
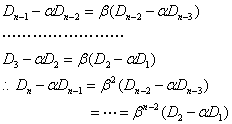（递推计算）
直接计算
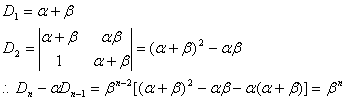
若
；否则，除以
后移项：
再一次用递推计算：
∴
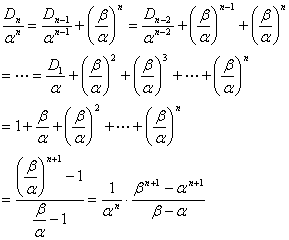
，当β≠α（3）
当β = α，从
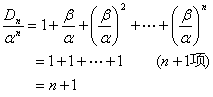
从而
。
由（3）式，若
。
∴
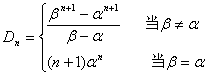
注递推式（2）通常称为常系数齐次二阶线性差分方程.
注1仿照例1的讨论，三对角线型的n阶行列式
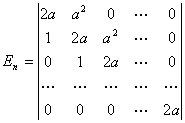（3）
和三对角线型行列式
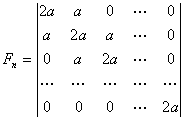（4）
有相同的递推关系式
（5）
（6）
注意
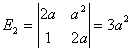
两个序列
和
的起始值
相同，递推关系式（5）和（6）的构造也相同，故必有
由（4）式，
的每一行都能提出一个因子a，故等于
乘一个n阶行列式，这一个行列式就是例1的。前面算出
，故
例2 计算n阶范德蒙行列式行列式
解:
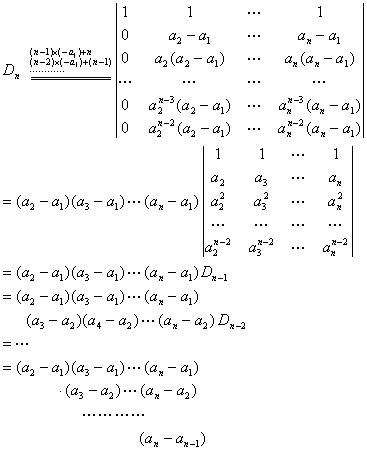
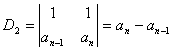
即n阶范德蒙行列式等于
这n个数的所有可能的差
的乘积
2．拆元法
例3：计算行列式
解
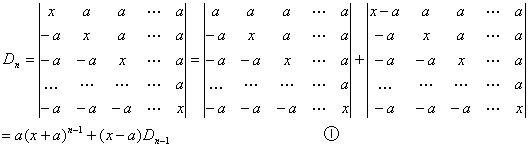
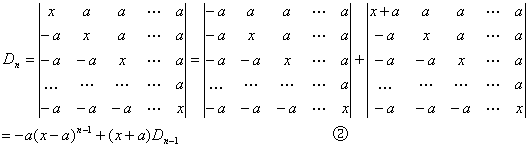
①×（x + a）
②×（x – a）
3．加边法
例4计算行列式
分析：这个行列式的特点是除对角线外,各列元素分别相同.根据这一特点,可采用加边法.
解
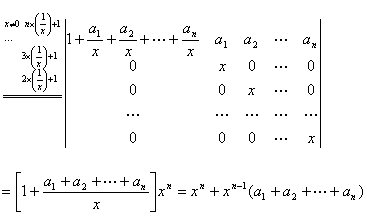
4．数学归结法
例5计算行列式
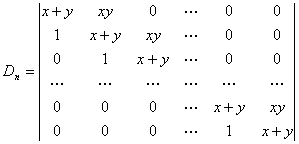
解：
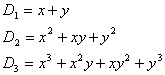
猜测：
证明
（1）n = 1, 2, 3 时，命题成立。假设n≤k – 1 时命题成立,考察n=k的情形：
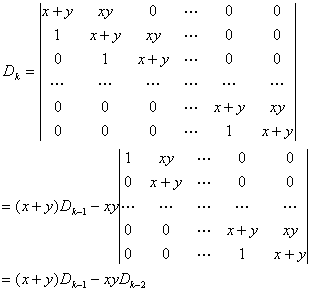
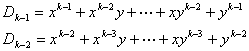
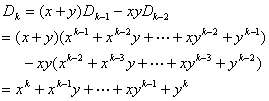
故命题对一切自然数n成立。
5.消去法求三对角线型行列式的值
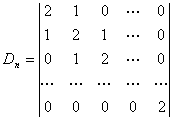
例6求n阶三对角线型行列式的值：
（1）
的构造是：主对角线元全为2，主对角线上方第一条次对角线与下方第一条次对角线的元全为1，其余的元全为0。
解用消去法，把中主对角线下方第一条次对角线的元1全部消成0：首先从第二行减去第一行的
倍，于是第二行变为
其次从第三行减去第二行（指新的第二行，以下同）的
倍，则第三行变为
再从第四行减去第三行的
倍，则第四行变为
类似地做下去，直到第n行减去第n – 1行的
倍，则第n行变为
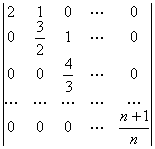
最后所得的行列式为
（2）
上面的行列式是三角型行列式，它的主对角线元顺次为
93）
又主对角线下方的元全为0。故的值等于（3）中各数的连乘积，即。
注3一般的三对角线型行列式
（4）
也可以按上述消去法把次对角线元
全部消去，得到一个三角型行列式，它的值等于该三角型行列式的主对角线元的连乘积。
6 乘以已知行列式
例7求行列式的值：
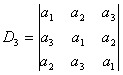
称为循环行列式，各行自左到右均由
循环排列而得，并使主对角线元全为
解设1的立方根为
，即
其中i是虚数单位，又
右乘以行列式
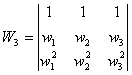
则
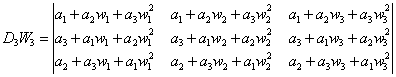（1）
用
，得
故（1）的行列式的第一列可由提出公因子
，提后的元顺次为
，类似地，（1）的行列式的第二列和第三列可提出公因子
和
于是
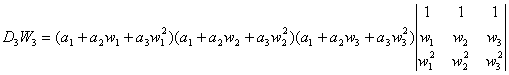
因互不相等，帮它们所构成的凡德蒙行列式
的值不为零，可以从上式的左右两边约去，得
。
注4在n阶的一般情形，设1的n次方根为
则得行列式的值为
这里的是由构成的n阶循环行列式：
7 利用线性代数方程组的解
例8求n阶行列式的值：
（1）
的构造是：第i行的元顺次为
又第n行的元顺次为
。
解（1）的行列式与凡德蒙行列式
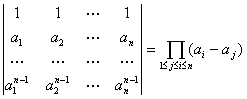（2）
的比值可以看成线性代数方程组
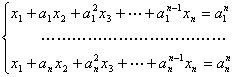（3）
的解
。如能解出，乘以凡德蒙行列式（2），即是原行列式
但方程组（3）又可以看成n次多项式方程
（4）
（t是未知数，
看作系数）有n个根
用根与系数的关系，即得
∴
8 递推方程组方法
例9求行列式的值：
（1）
是n阶行列式（在右下角用（n）表示），其结构是：主对角线元全为x ；主对角线上方的元全为y , 下方的元全为z 。
解从（1）的行列式的第一列减第二列，第二列减第三列，…，第n – 1列减第n列，得
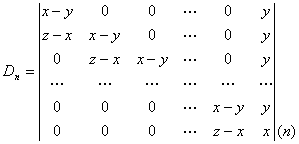（2）
上面的行列式按第一行展开，有两项，一项是（x – y）乘一个n – 1阶行列式，这个n – 1阶行列式和（2）中的n阶行列式的构造相同，即上述展开的第一项可表示为
；展开的另一项是
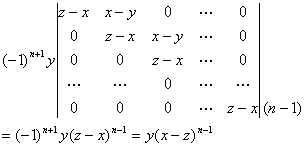
故递推式
（3）
若z = y，则上式化为
（4）
类似地有
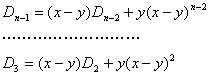
又
故可对（4）式递推计算如下：
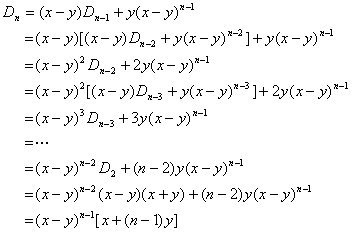
上面得到原行列式当z = y时的值。下面讨论z≠y的情形。
把（1）的行列式的y与z对调，这相当于原行列式的行与列互换，这样的做法，行列式的值不变。于是y和z对调后，
的值不变，这时（3）式变为
（5）
从（3）与（5）（递推方程组）消去
，即（3）式乘以（x – z），（5）乘以（x – y），相减得
∴
注5当z = y时，行列式也可以用极限计算：
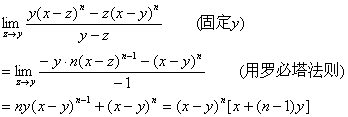
又行列式当z = y时可以用余式定理来做。