第六章 向量空间
§6.1 定义和例子
1.令F是一个数域,在F3里计算
(i)![]() (2,0,-1)+(-1,-1,2)+
(2,0,-1)+(-1,-1,2)+![]() (0,1,-1);
(0,1,-1);
(ii)5(0,1,-1)-3(1,![]() ,2)+(1,-3,1).
,2)+(1,-3,1).
2.证明:如果
a(2,1,3)+ b(0,1,2)+ c(1,-1,4)=(0,0,0),
那么a = b = c = 0.
3.找出不全为零的三个有理数a,b,c(即a,b,c中至少有一个不是0),使得
a (1,2,2) + b(3,0,4)+ c (5,-2,6) = (0,0,0).
4.令![]() 1 = (1,0,0),
1 = (1,0,0),![]() 2 = (0,1,0),
2 = (0,1,0),![]() 3 =(0,0,1).证明,R3中每一个向量
3 =(0,0,1).证明,R3中每一个向量![]() 可以唯一地表示为
可以唯一地表示为
![]() = a1
= a1![]() 1 + a2
1 + a2![]() 2 + a3
2 + a3![]() 3
3
形式,这里a1,a2,a3 ![]() R.
R.
5.证明,在数域F上向量空间V里,以下算律成立:
(i)a (![]() ) = a
) = a![]() - a
- a![]() ;
;
(ii) (a- b) ![]() = a
= a![]() - b
- b![]() , 这里a,b
, 这里a,b![]() F ,
F ,![]() ,
,![]()
![]() V.
V.
6.证明:数域F上一个向量空间如果含有一个非零向量,那么它一定含有无限多个向量.
7.证明,对于任意正整数n 和任意向量![]() ,都有
,都有
n![]() =
=![]() +…+
+…+![]() .
.
8.证明,向量空间定义中条件3º,8)不能由其余条件推出.
9.验证本节最后的等式:
(![]() 1,…,
1,…,![]() n)(AB) =((
n)(AB) =((![]() 1,…,
1,…,![]() n)A)B.
n)A)B.
§6.2 子空间
1.判断R n中下列子集哪些是子空间:
{(a1,0,…,0,an)| a1,an
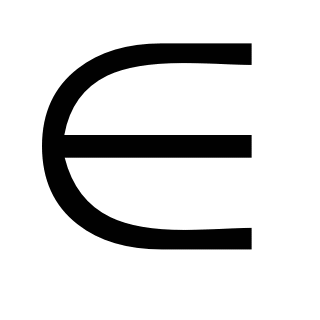 R};
R};{(a1 ,a2 ,…,an )|
 ai =0};
ai =0};{(a1 ,a2 ,…,an )|
 ai =1};
ai =1};{(a1 ,a2 ,…,an )| ai
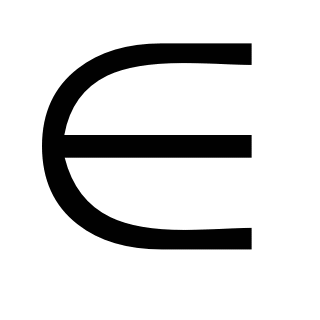 Z,i = 1,…,n}.
Z,i = 1,…,n}.
2.Mn (F)表示数域F上一切n阶矩阵所组成的向量空间(参看6.1,例2)令
S={ A![]() Mn (F) |A′= A},
Mn (F) |A′= A},
T={ A![]() Mn (F) |A′= –A}.
Mn (F) |A′= –A}.
证明,S和T都是 Mn (F)的子空间,并且
Mn(F) = S + T,S ![]() T={0}.
T={0}.
3.设W1,W2是向量空间V的子空间,证明:如果V的一个子空间既包含W1又包含W2,那么它一定包W1 +W2.在这个意义下,W1+W2是V的既含W1又含W2的最小子空间.
4.设V是一个向量空间,且V![]() {0}.证明:V不可能表成它的两个真子空间的并集.
{0}.证明:V不可能表成它的两个真子空间的并集.
5.设W,W1,W2都是向量空间V的子空间,其中W1![]() W2且W
W2且W![]() W1=W
W1=W![]() W2,
W2,
W + W1=W + W2.证明:W1=W2.
6.设W1,W 2是数域F上向量空间V的两个子空间,![]() ,
,![]() 是V的两个向量,其中
是V的两个向量,其中![]()
![]() W2,但
W2,但![]()
![]() W1,又
W1,又![]()
![]() W2,证明:
W2,证明:
对于任意k
 F,
F,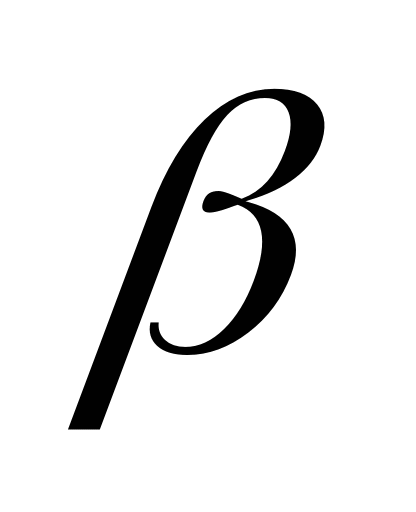 +k
+k
 W2;
W2;至多有一个k
 F,使得
F,使得 +k
+k
 W1 .
W1 .
7.设W1,W2,…,Wr 是向量空间V的子空间,且Wi ![]() V,i=1,…,r.
V,i=1,…,r.
证明:存在一个向量![]()
![]() V,使得
V,使得![]()
![]() Wi, i=1,…,r.
Wi, i=1,…,r.
[提示:对r作数学归纳法并且利用第6题的结果.]
§6.3 向量的线性相关性
1.下列向量组是否线性相关:
(i)(3,1,4),(2,5,-1),(4,-3,7);
(ii) (2,0,1),(0,1,-2),(1,-1,1);
(iii) (2,-1,3,2),(-1,2,2,3),(3,-1,2,2),(2,-1,3,2).
2.证明,在一个向量组{![]() }里,如果有两个向量
}里,如果有两个向量![]() 与
与![]() 成比例,即
成比例,即![]() =k
=k![]() ,
,![]() ,那么{
,那么{![]() }线性相关.
}线性相关.
3.令![]()
![]() 。证明
。证明![]() 线性相关必要且只要行列式
线性相关必要且只要行列式
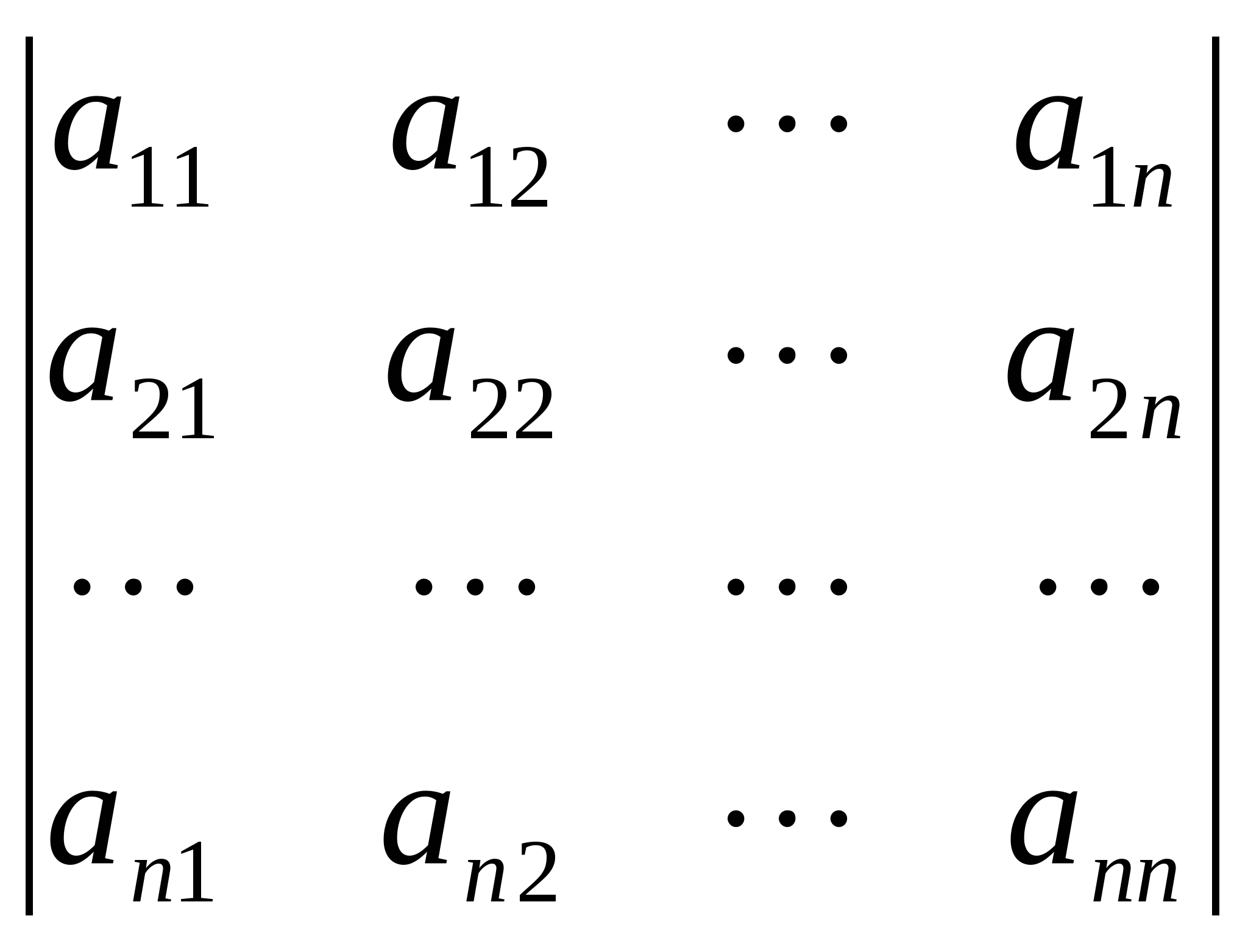 = 0.
= 0.
4.设![]()
![]() ,线性无关.对每一个
,线性无关.对每一个![]() 任意添上p个数,得到
任意添上p个数,得到![]() 的m个向量
的m个向量![]()
![]() .
.
证明{![]() 1,
1,![]() 2 ,…,
2 ,…,![]() m}也线性无关
m}也线性无关
5.设![]() 线性无关,证明
线性无关,证明![]() 也线性无关.
也线性无关.
6.设向量组{![]() } (
} (![]() 线性无关,任取
线性无关,任取![]() .证明,向量组
.证明,向量组![]() 线性无关.
线性无关.
7.下列论断哪些是对的,哪些是错的,如果是对的,证明;如果是错的,举出反例:
(i) 如果当![]() ,那么
,那么![]() 线性无关.
线性无关.
(ii) 如果![]() 线性无关,而
线性无关,而![]() 不能由
不能由![]() 线性表示,那么
线性表示,那么![]() ,
,![]() 也线性无关.
也线性无关.
(iii) 如果![]() 线性无关,那么其中每一个向量都不是其余向量的线性组合.
线性无关,那么其中每一个向量都不是其余向量的线性组合.
(iv) 如果![]() 线性相关,那么其中每一个向量都是其余向量的线性组合.
线性相关,那么其中每一个向量都是其余向量的线性组合.
8.设向量![]() 可以由
可以由![]() 表示,但不能由
表示,但不能由![]() 线性表示.证明,向量组{
线性表示.证明,向量组{![]() }与向量组{
}与向量组{![]() ,
,![]() }等价.
}等价.
9.设向量组![]() 中
中![]() 并且每一
并且每一![]() 都不能表成它的前
都不能表成它的前![]() 个向量
个向量![]() 的线性组合.证明
的线性组合.证明![]() 线性无关.
线性无关.
10.设向量![]() 线性无关,而
线性无关,而![]() ,
,![]() ,
,![]() 线性相关,证明,或者
线性相关,证明,或者![]() 与
与![]() 中至少有一个可以由
中至少有一个可以由![]() 线性表示,或者向量组{
线性表示,或者向量组{![]() ,
,![]() }与{
}与{![]() ,
,![]() }等价.
}等价.
§6.4 基和维数
1.令Fn [x]表示数域F上一切次数![]() n的多项式连同零多项式所组成的向量空间.这个向量空间的维数是几?下列向量组是不是F3[x]的基:
n的多项式连同零多项式所组成的向量空间.这个向量空间的维数是几?下列向量组是不是F3[x]的基:
![]() (i){x3+1,x+1,x2+x,x3+x2+2x+2};
(i){x3+1,x+1,x2+x,x3+x2+2x+2};
(ii){x-1,1-x2,x2+2x-2,x3}.
2.求下列子空间的维数:![]()
(i)L ( (2,-3,1),(1,4,2),(5,-2,4))![]() R3
R3
(ii)L(x-1,1-x2,x2-x)![]() F[x];
F[x];
(iii)L(ex,e2x,e3x)![]() C [a,b].
C [a,b].
3.把向量组{(2,1,-1,3),(-1,0,1,2)}扩充为R4的一个基.
4.令S是数域F上一切满足条件A’=A的n阶矩阵A所成的向量空间,求S的维数.
5.证明,复数域C作为实数域R上向量空间,维数是2.如果C看成它本身上的向量空间的话,维数是几?
6.证明定理6.4.2的逆定理:如果向量空间V的每一个向量都可以唯一地表成V中向量
![]() 的线性组合,那么dimV = n.
的线性组合,那么dimV = n.
7.设W是R n 的一个非零子空间,而对于W的每一个向量(a1,a2,…,an)来说,要么a1 = a2= … = an = 0,要么每一个ai都不等于零,证明dimW = 1.
8.设W是n维向量空间V的一个子空间,且0< dimW < n.证明:W在V中有不只一个余子空间.
9.证明本书最后的论断.
§6.5 坐标
1.设{![]() 1 ,
1 ,![]() 2,…,
2,…,![]() n}是V的一个基.求由这个基到{
n}是V的一个基.求由这个基到{![]() 2 ,…,
2 ,…,![]() n,
n,![]() 1}的过渡矩阵.
1}的过渡矩阵.
2.证明,{x3,x3+x,x2+1,x+1}是F3 [x](数域F上一切次数![]() 3的多项式及零)的一个基.求下列多项式关于这个基的坐标:
3的多项式及零)的一个基.求下列多项式关于这个基的坐标:
(i)x2+2x+3;(ii)x3; (iii)4;(iv)x2-x.
3.设![]() 1 =(2,1,-1,1),
1 =(2,1,-1,1),![]() 2=(0,3,1,0),
2=(0,3,1,0),![]() 3=(5,3,2,1)
3=(5,3,2,1)![]() 4=(6,6,1,3).证明{
4=(6,6,1,3).证明{![]() 1 ,
1 ,![]() 2,
2,![]() 3,
3,![]() 4 } 作成R4的一个基.在R4中求一个非零向量,使它关于这个基的坐标与关于标准基的坐标相同.
4 } 作成R4的一个基.在R4中求一个非零向量,使它关于这个基的坐标与关于标准基的坐标相同.
4.设
![]() 1 =(1,2,-1),
1 =(1,2,-1),![]() 2=(0,-1,3),
2=(0,-1,3),![]() 3=(1,-1,0);
3=(1,-1,0);
![]() 1=(2,1,5),
1=(2,1,5),![]() 2=(-2,3,1),
2=(-2,3,1),![]() 3=(1,3,2).
3=(1,3,2).
证明{![]() 1 ,
1 ,![]() 2,
2,![]() 3 }和{
3 }和{![]() 1,
1,![]() 2 ,
2 ,![]() 3}都是R3的基.求前者到后者的过渡矩阵.
3}都是R3的基.求前者到后者的过渡矩阵.
5.设{![]() 1 ,
1 ,![]() 2,…,
2,…,![]() n}是F上n维向量空间V的一个基.A是F上一个n
n}是F上n维向量空间V的一个基.A是F上一个n![]() s矩阵.令
s矩阵.令
(![]() 1,
1,![]() 2 ,…,
2 ,…,![]() s)=(
s)=(![]() 1 ,
1 ,![]() 2,…,
2,…,![]() n)A.
n)A.
证明
dimL(![]() 1,
1,![]() 2 ,…,
2 ,…,![]() s)=秩A.
s)=秩A.
§6.6 向量空间的同构
1.证明,复数域C作为实数域R上向量空间,与V2同构.
2.设![]() 是向量空间V到W的一个同构映射,V1是V的一个子空间.证明
是向量空间V到W的一个同构映射,V1是V的一个子空间.证明![]() 是W的一个子空间.
是W的一个子空间.
3.证明:向量空间![]() 可以与它的一个真子空间同构.
可以与它的一个真子空间同构.
§6.7 矩阵的秩 齐次线性方程组的解空间
1.证明:行列式等于零的充分且必要条件是它的行(或列)线性相关.
2.证明,秩(A+B)![]() 秩A+秩B.
秩A+秩B.
3.设A是一个m行的矩阵,秩A=r,从A中任取出s行,作一个s行的矩阵B.证明,秩B![]() r+s – m.
r+s – m.
4.设A是一个m![]() n矩阵,秩A=r.从A中任意划去m–s行与n–t列,其余元素按原来位置排成一个s
n矩阵,秩A=r.从A中任意划去m–s行与n–t列,其余元素按原来位置排成一个s![]() t矩阵C,证明,秩C
t矩阵C,证明,秩C![]() r+s+t–m–n.
r+s+t–m–n.
5.求齐次线性方程组
x1 + x2 + x3 + x4 + x5=0,![]()
3x1 +2x2 + x3 +x4 –3x5=0,
5x1 + 4 x2 + 3x3 +3x4–x5=0,
x2 + 2x3 + 2x4+ x5=0![]()
的一个基础解系.
6.证明定理6.7.3的逆命题:Fn的任意一个子空间都是某一含n个未知量的齐次线生方程组的解空间.
7.证明,Fn的任意一个≠Fn的子空间都是若干n–1维子空间的交.