第七章 线性变换
§7.1 线性映射
1．令
=（x1，x2，x3）是R3的任意向量．下列映射
哪些是R3到自身的线性映射？
（1）() = + 
，是R3的一个固定向量．
（2）() = (2x1–x2 + x3，x2 + x3，–x3)
（3）() =（x12，x22，x32）．
（4）() =（cosx1，sinx2，0）．
2．设V是数域F上一个一维向量空间．证明V到自身的一个映射是线性映射的充要条件是：对于任意
V，都有() = a，这里a是F中一个定数．
3．令Mn (F) 表示数域F上一切n阶矩阵所成的向量空间．取定AMn(F).对任意XMn (F)，定义
(X) = AX–XA．
证明：
是Mn (F)是自身的线性映射。证明：对于任意X，Y
Mn (F)，
(XY) = (X)Y+X(Y) ．
4．令F4表示数域F上四元列空间，取
A=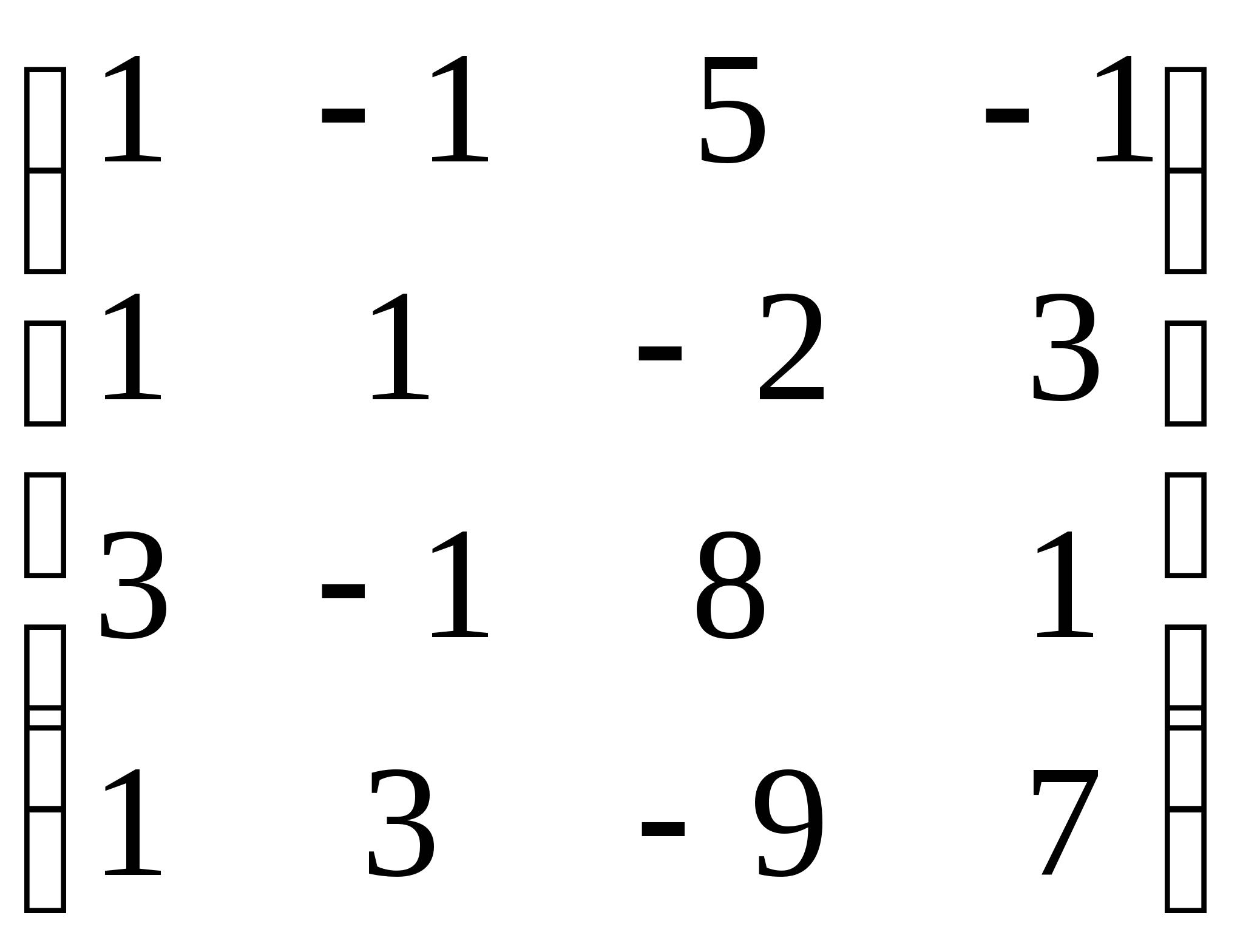
对于F4，令() = A．求线性映射的核和像的维数．
5．设V和W都是数域F上向量空间，且dimV = n．令是V到W的一个线性映射．我们如此选取V的一个基：
1，…，s，s+1，…，n，使得1，…，s，是Ker()的一个基．证明：
（i）(s+1)，…，(n)组成Im()的一个基；
（ii）dim Ker() + dim Im() = n.。
6．设是数域F上n维向量空间V到自身的一个线性映射．W1，W2是V的子空间，并且V = W1
W2．证明：有逆映射的充要条件是V = (W1)(W1) ．
§7.2 线性变换的运算
1．举例说明，线性变换的乘法不满足交换律．
2．在F[x]中，定义
：f (x) 
f’(x) ，
：f (x)xf (x) ，
这里f’(x)表示f(x)的导数．证明,,都是F[x]的线性变换，并且对于任意正整数n都有
n–n = nn-1
3．设V是数域F上的一个有限维向量空间．证明，对于V的线性变换来说，下列三个条件是等价的：
（i）是满射； (ii)Ker() = {0}; (iii)非奇异．
当V不是有限维时，(i)，(ii)是否等价？
4．设L (V)，V，并且，()，…，k-1()都不等于零，但k() = 0．证明：
，()，…，k-1()
线性无关．
5．L (V) ．证明
(1) Im()
Ker()当且仅当 2 = 
；
Ker(
)Ker(2)Ker(3)…；Im(
)
Im(2)Im(3)…．
6．设Fn = { (x1，x2，…，xn ) | xiF }是数域F上n 维行空间．定义
(x1，x2，…，xn ) = (0，x1，…，xn-1 ) ．
(i) 证明：是Fn的一个线性变换，且 n = ；
(ii) 求Ker()和Im() 的维数．
§7.3 线性变换和矩阵
1．令Fn[x]表示一切次数不大于n的多项式连同零多项式所成的向量空间，：f (x) f’(x) ，求关于以下两个基的矩阵：
(1) 1，x ，x2，…，xn，
(2) 1，x–c，
，…，
，cF．
2．设F上三维向量空间的线性变换关于基 {1，2，3}的矩阵是
求关于基
1 = 21 +32 +3，
2 = 31 +42 +3，
3 = 1 +22 +23，
的矩阵．
设= 21 +2–3．求()关于基1，2，3的坐标．
3．设{
1，2，…，n}是n维向量空间V的一个基．
j = 
，
= 
， j = 1，2，…，n，
并且1，2，…，n线性无关．又设是V的一个线性变换，使得(j) = ，j = 1，2，…，n，求关于基
，
，…，
的矩阵．
4．设A，B是n阶矩阵，且A可逆，证明，AB与BA相似．
5．设A是数域F上一个n阶矩阵，证明，存在F上一个非零多项式f (x)使得f (A) = 0．
6．证明，数域F上n维向量空间V的一个线性变换是一个位似（即单位变换的一个标量倍）必要且只要关于V的任意基的矩阵都相等．
7．令Mn (F)是数域F上全休n阶矩阵所成的向量空间．取定一个矩阵AMn(F) ．对任意XMn (F)，定义
(X) = AX–XA．
由7.1习题3知是Mn (F)的一个线性变换，设
A =
是一个对角形矩阵．证明，关于Mn (F)的标准基{Eij |1
}(见6.4，例5)的矩阵也是对角形矩阵，它的主对角线上的元素是一切ai–aj(1).[建议先具体计算一下n = 3的情形．]
8．设是数域F上n维向量空间V的一个线性变换．证明，总可以如此选取V的两个基{1，2，…，n}和{1，2，…，n}，使得对于V的任意向量来说，如果=
，则() =
，这里0
是一个定数[提示：利用7.1，习题5选取基1，2，…，n．]
§7.4 不变子空间
1．设是有限维向量空间V的一个线性变换，而W是的一个不变子空间，证明，如果 有逆变换，那么W也在-1之下不变．
2．设
是向量空间V的线性变换，且
．证明Im()和Ker()都在之下不变．
3．是数域F上向量空间V的一个线性变换，并且满足条件2 =．证明：
(i) Ker() = {
}；
(ii)V = Ker()Im()；
(iii)如果是V的一个线性变换，那么Ker()和Im()都在之下不变的充要条件是．
4．设是向量空间V的一个位似（即单位变换的一个标量倍）．证明，V的每一个子空间都在之下不变．
5．令S是数域F上向量空间V的一些线性变换所成的集合．V的一个子空间W如果在S中每一线性变换之下不变，那么就说W是S的一个不变子空间．S说是不可约的，如果S在V中没有非平凡的不变子空间，设S不可约，而
是V的一个线性变换，它与S中每一线性变换可交换。证明或者是零变换，或者是可逆变换．[提示：令W = Ker.证明W是要的一个不变子空间．]
§7.5 本征值和本征向量
1．求下列矩阵在实数域内的特征根和相应的特征向量：
(i) 
； (ii) 
；(iii) 
．
2．证明：对角形矩阵
与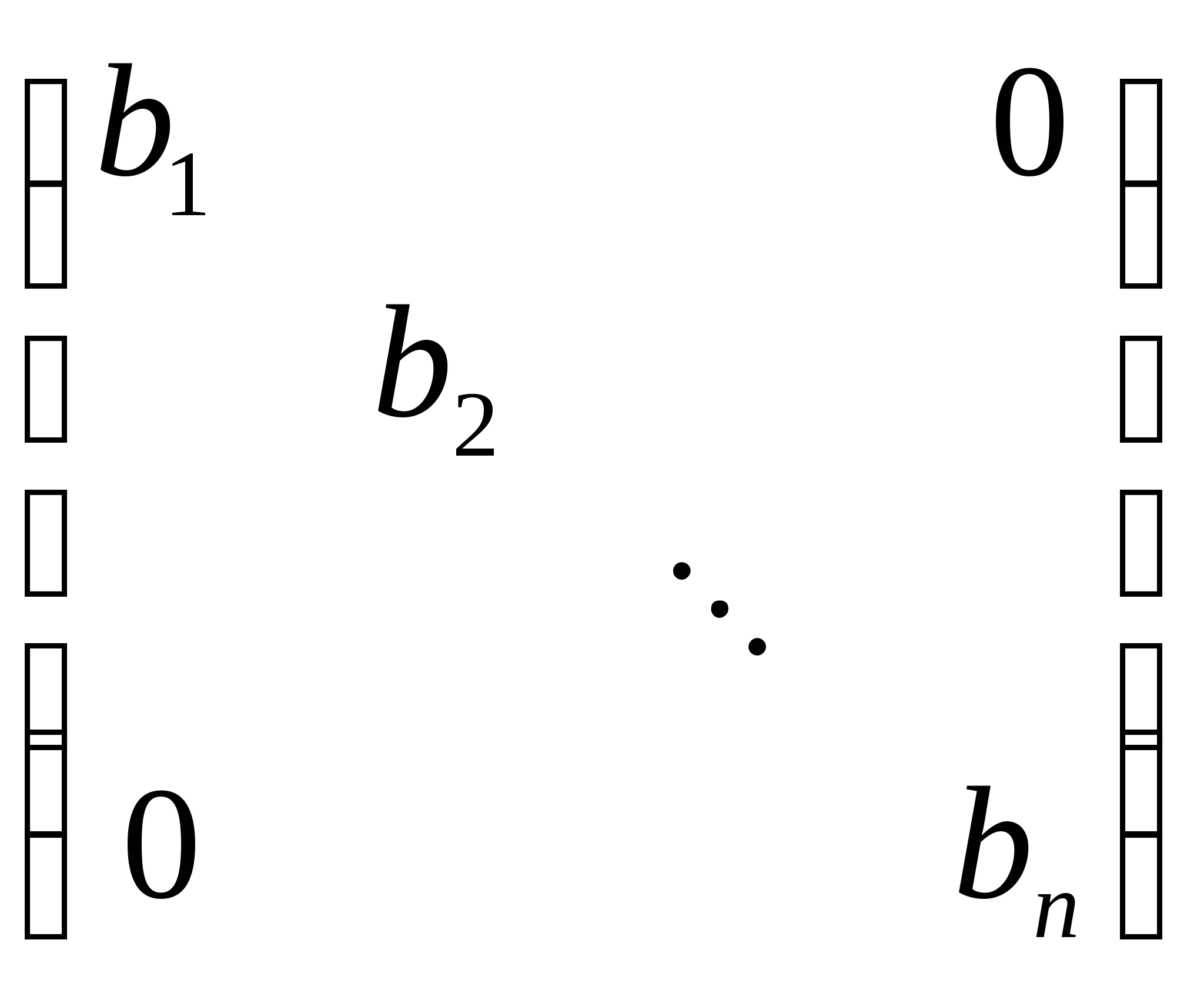
相似必要且只要b1，b2，…，bn是a1，a2，…，an的一个排列．
3．设
A = 
是一个实矩阵且ad–bc = 1 ．证明：
(i) 如果| trA |>2，那么存在可逆实矩阵T，使得
T-1AT = 
．
这里
且
，1，-1．
(ii) 如果| trA | = 2且A
，那么存在可逆实矩阵T，使得
T-1AT = 
或
.．
(iii) 如果| trA | < 2则存在可逆实矩阵T及
，使得
T-1AT = 
．
[提示] 在(iii)，A有非实共轭复特征根
=1.将
写成三角形式．令
是A的属于的一个特征向量，计算A
和A
．
4．设a，b，c
．令
A=
，B=
，C=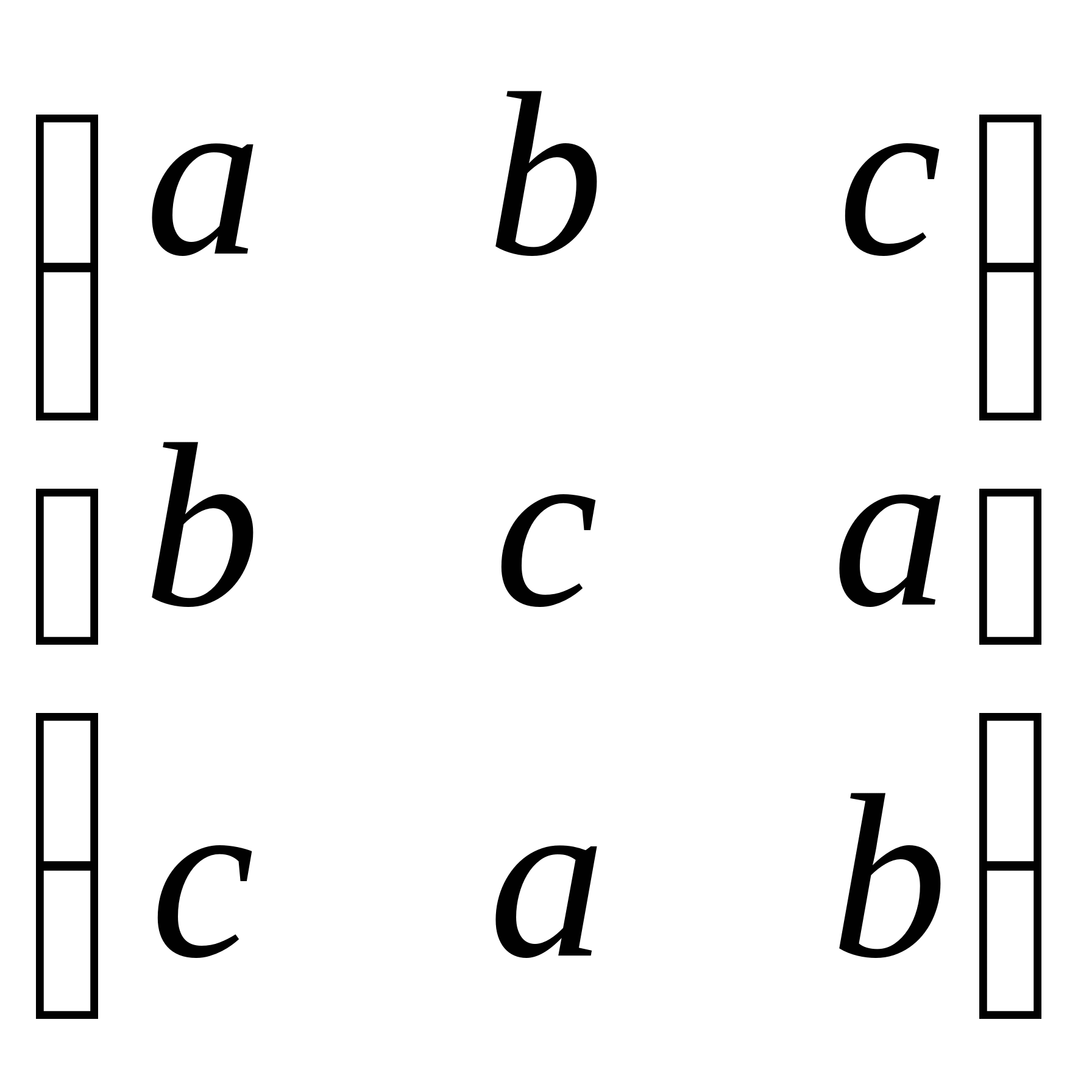
．
(i) 证明，A，B，C彼此相似；
(ii) 如果BC=CB，那么A，B，C的特征根至少有两个等于零．
5．设A是复数域C上一个n阶矩阵．
(i) 证明：存在C上n阶可逆矩阵T使得
T-1AT =
．
(ii) 对n作数学归纳法证明，复数域C上任意一个n阶矩阵都与一个“上三角形”矩阵
相似，这里主对角线以下的元素都是零．
6．设A是复数域C上一个n阶矩阵，
是A的全部特征根（重根按重数计算）．
(i) 如果f (x)是C上任意一个次数大于零的多项式，那么f (
是f(A)的全部特征根．
(ii) 如果A可逆，那么
，并且
是A-1的全部特征根
7．令
A = 
是一个n阶矩阵。
(i) 计算
．
(ii) 求A的全部特征根．
8．
是任意复数，行列式
D = 
叫做一个循环行列式，证明：
D = 
，
这里
，而
是全部n次单位根．[提示：利用6.7两题的结果．]
9．设A，B是复数域上n阶矩阵．证明，AB与BA有相同的特征根，并且对应的特征根的重数也相同．[提示：参看5.3习题2．]
§7.6 可以对角化的矩阵
1．检验7.5习题1中的矩阵哪些可以对角化．如果可以对角化，求出过渡矩阵T．
2．设 
，
求A10．
3．设是数域F上n维向量空间V的一个线性变换．令
是的两两不同的本征值，
是属于本征值
的本征子空间．证明，子空间的和
是直和，并在之下不变．
4．数域F上n维向量空间V的一个线性变换叫做一个对合变换，如果2 =ι,ι,是单位变换，设是V的一个对合变换，证明:
(i) 的本征值只能是
；
(ii) V = V1
，这里V1是的属于本征值1的本征子空间，V
是的属于本征值 –1 的本征子空间．[提示：设
]
5．数域F上一个n 阶矩阵A叫做一个幂等矩阵，如果
,设A是一个幂等矩阵.证明：
(i)I + A 可逆，并且求
．
(ii)秩A + 秩
[提示：利用7.4，习题3 (ii)．]
6．数域F上n维向量空间V的一个线性变换叫做幂零的，如果存在一个自然数m使m = 0.证明：
(i) 是幂零变换当且仅当它的特征多项式的根都是零；
(ii) 如果一个幂零变换可以对角化，那么一定是零变换．
7．设V是复数域上一个n维向量空间，S是V的某些线性变换所成的集合，而是V的一个线性变换，并且与S中每一线性变换可交换，证明，如果S不可约 (参看7.4，习题5)，那么一定是一个位似． [提示：令是的一个本征值，考虑的属于的本征子空间，并且利用7.4，习题5的结果．]
8．设是数域F上n维向量空间V的一个可以对角化的线性变换，令
是的全部本征值．证明，存在V的线性变换
，使得
(i) 
；
(ii) 
(iii) 
(iv) 
(v) 
的属于本征值的本征子空间，
9．令V是复数域C上一个n维向量空间，，是V的线性变换，且．
(i) 证明，的每一本征子空间都在之下不变；
(ii) 与在V中有一公共本征向量．