第八章 欧氏空间和酉空间
§8.1向量的内积
1.证明:在一个欧氏空间里,对于任意向量![]() ,以下等式成立:
,以下等式成立:
(1)![]() ;
;
(2)![]()
在解析几何里,等式(1)的几何意义是什么?
2.在区氏空间![]() 里,求向量
里,求向量![]() 与每一向量
与每一向量
![]() ,
,![]()
的夹角.
3.在欧氏空间![]() 里找出两个单位向量,使它们同时与向量
里找出两个单位向量,使它们同时与向量
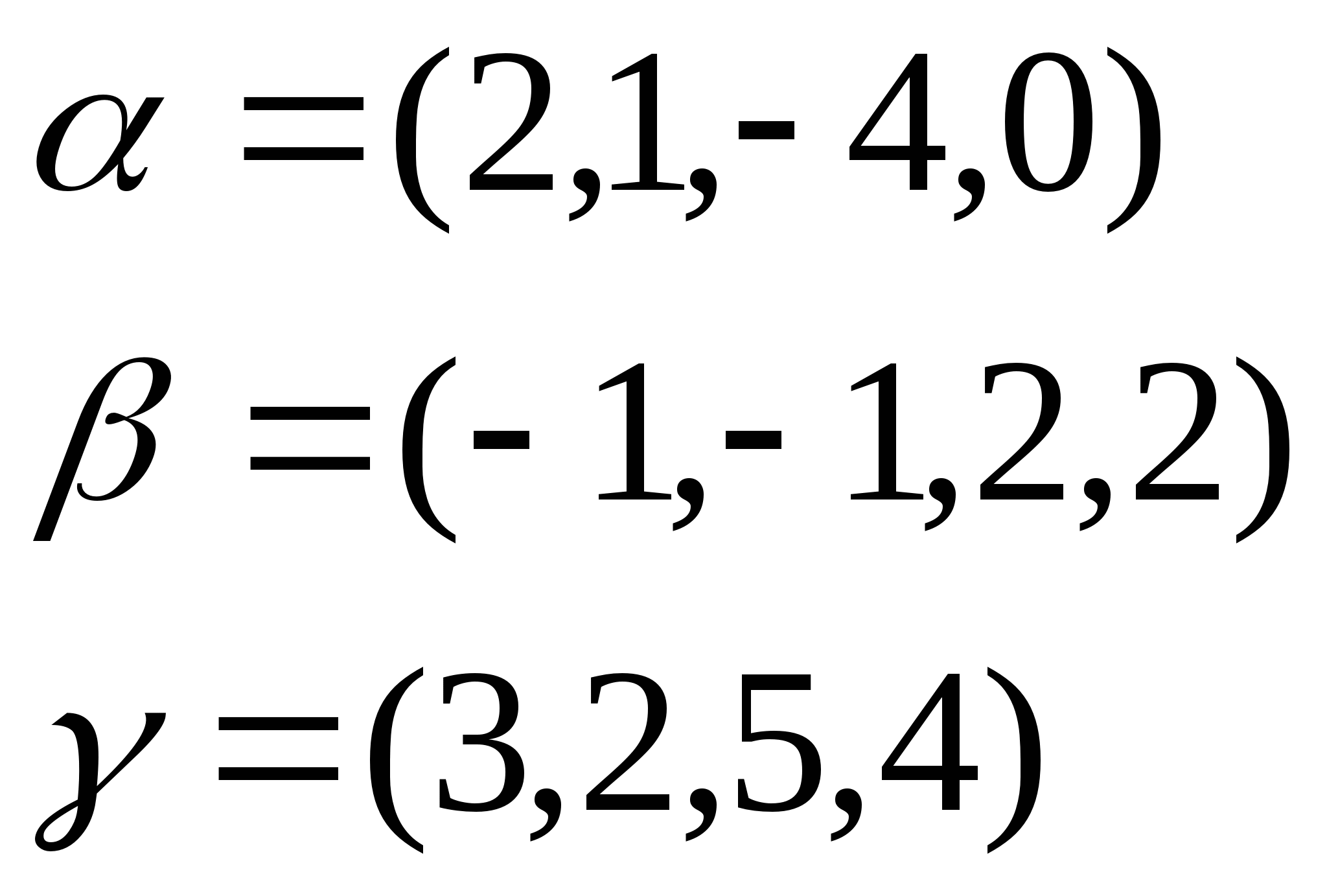
中每一个正交.
4.利用内积的性质证明,一个三角形如果有一边是它的外接圆的直径,那么这个三角形一定是直角三角形.
5.设![]() 是一个欧氏空间里彼此正交的向量.证明:
是一个欧氏空间里彼此正交的向量.证明:
![]() (勾股定理)
(勾股定理)
6.设![]() 都是一个欧氏空间的向量,且
都是一个欧氏空间的向量,且![]() 是
是![]() 的线性组合.证明,如果
的线性组合.证明,如果![]() 与
与![]() 正交,
正交,![]() ,那么
,那么![]() .
.
7.设![]() 是欧氏空间的
是欧氏空间的![]() 个向量.行列式
个向量.行列式

叫做![]() 的格拉姆(Gram)行列式.证明
的格拉姆(Gram)行列式.证明![]() =0,必要且只要
=0,必要且只要![]() 线性相关.
线性相关.
8.设![]() 是欧氏空间两个线性无关的向量,满足以下条件:
是欧氏空间两个线性无关的向量,满足以下条件:
![]() 和
和![]() 都是
都是![]() 的整数.
的整数.
证明:![]() 的夹角只可能是
的夹角只可能是![]() .
.
9.证明:对于任意实数![]() ,
,
![]() ).
).
§8.2 正交基
1.已知
![]() ,
,![]()
![]() ,
,![]()
是![]() 的一个基.对这个基施行正交化方法,求出
的一个基.对这个基施行正交化方法,求出![]() 的一个规范正交基.
的一个规范正交基.
2.在欧氏空间![]() 里,对于线性无关的向量级{1,
里,对于线性无关的向量级{1,![]() ,
,![]() ,
,![]() }施行正交化方法,求出一个规范正交组.
}施行正交化方法,求出一个规范正交组.
3.令![]() 是欧氏空间V的一组线性无关的向量,
是欧氏空间V的一组线性无关的向量,![]() 是由这组向量通过正交化方法所得的正交组.证明,这两个向量组的格拉姆行列式相等,即
是由这组向量通过正交化方法所得的正交组.证明,这两个向量组的格拉姆行列式相等,即
![]()
4.令![]() 是
是![]() 维欧氏空间V的一个规范正交基,又令
维欧氏空间V的一个规范正交基,又令
![]()
K叫做一个![]() -方体.如果每一
-方体.如果每一![]() 都等于0或1,
都等于0或1,![]() 就叫做K的一个项点.K的顶点间一切可能的距离是多少?
就叫做K的一个项点.K的顶点间一切可能的距离是多少?
5.设![]() 是欧氏空间V的一个规范正交组.证明,对于任意
是欧氏空间V的一个规范正交组.证明,对于任意![]() ,以下等式成立:
,以下等式成立:
![]() .
.
6.设V是一个![]() 维欧氏空间.证明
维欧氏空间.证明
![]() 如果W是V的一个子空间,那么
如果W是V的一个子空间,那么![]() .
.
![]() 如果
如果![]() 都是V的子空间,且
都是V的子空间,且![]() ,那么
,那么![]()
![]() 如果
如果![]() 都是V的子空间,那么
都是V的子空间,那么![]()
7.证明,![]() 中向量
中向量![]() 到平面
到平面
![]()
的最短距离等于
![]() .
.
8.证明,实系数线性方程组
![]()
有解的充分且必要条件是向量![]() 与齐次线性方程组
与齐次线性方程组
![]()
的解空间正交.
9.令![]() 是
是![]() 维欧氏空间V的一个非零向量.令
维欧氏空间V的一个非零向量.令
![]() .
.
![]() 称为垂直于
称为垂直于![]() 的超平面,它是V的一个
的超平面,它是V的一个![]() 维子空间.V中有两个向量
维子空间.V中有两个向量![]() ,
,![]() 说是位于
说是位于![]() 的同侧,如果
的同侧,如果![]() 同时为正或同时为负.证明,V中一组位于超平面
同时为正或同时为负.证明,V中一组位于超平面![]() 同侧,且两两夹角都
同侧,且两两夹角都![]() 的非零向量一定线性无关.
的非零向量一定线性无关.
[提示:设![]() 是满足题设条件的一组向量.则
是满足题设条件的一组向量.则![]() ,并且不妨设
,并且不妨设![]() .如果
.如果![]() ,那么适当编号,可设
,那么适当编号,可设![]() ,
,![]() ,令
,令![]() ,证明
,证明![]() .由此推出
.由此推出![]()
![]() .]
.]
10.设U是一个正交矩阵.证明:
![]() U的行列式等于1或-1;
U的行列式等于1或-1;
![]() U的特征根的模等于1;
U的特征根的模等于1;
![]() 如果
如果![]() 是U的一个特征根,那么
是U的一个特征根,那么![]() 也是U的一个特征根;
也是U的一个特征根;
![]() U的伴随矩阵
U的伴随矩阵![]() 也是正交矩阵.
也是正交矩阵.
11.设![]() ,且
,且
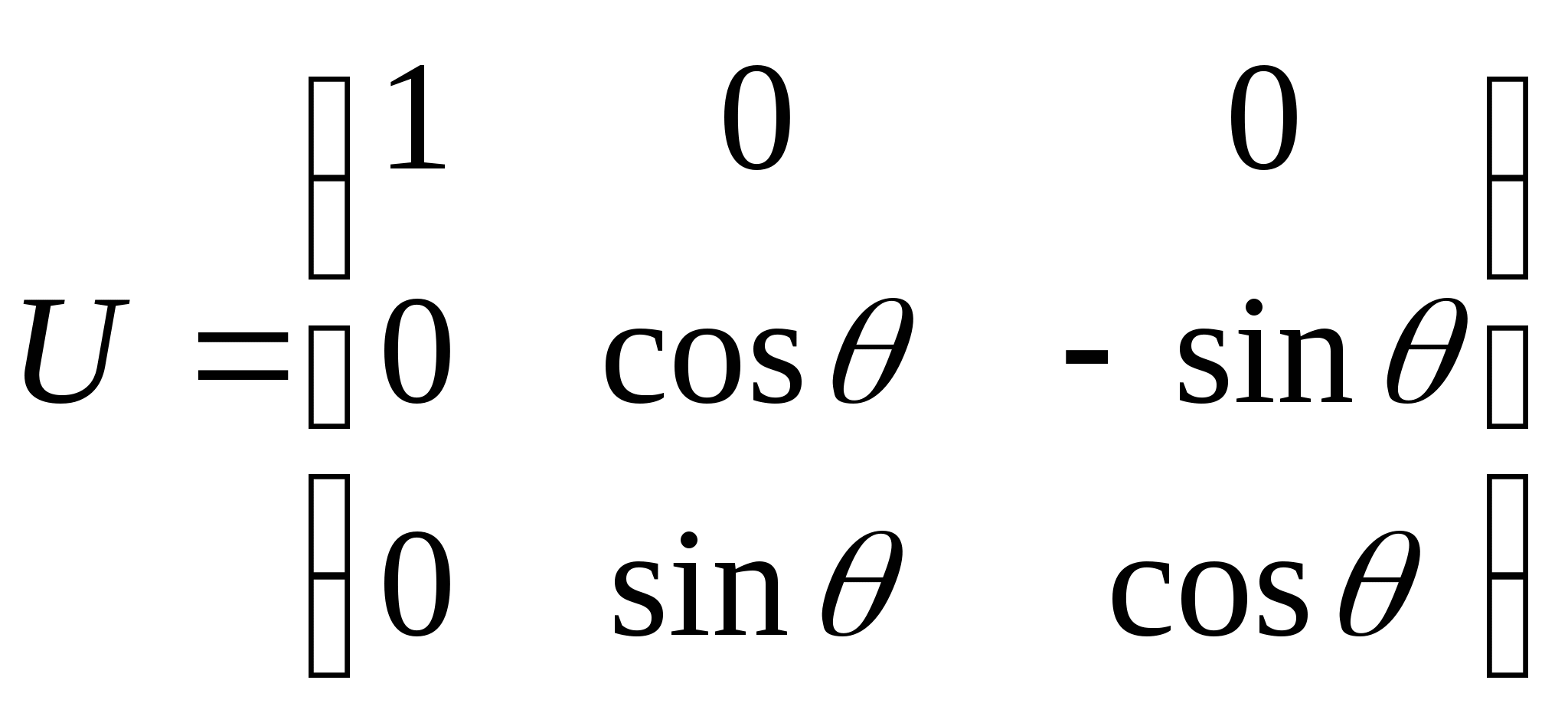 .
.
证明,![]() 可逆,并且
可逆,并且
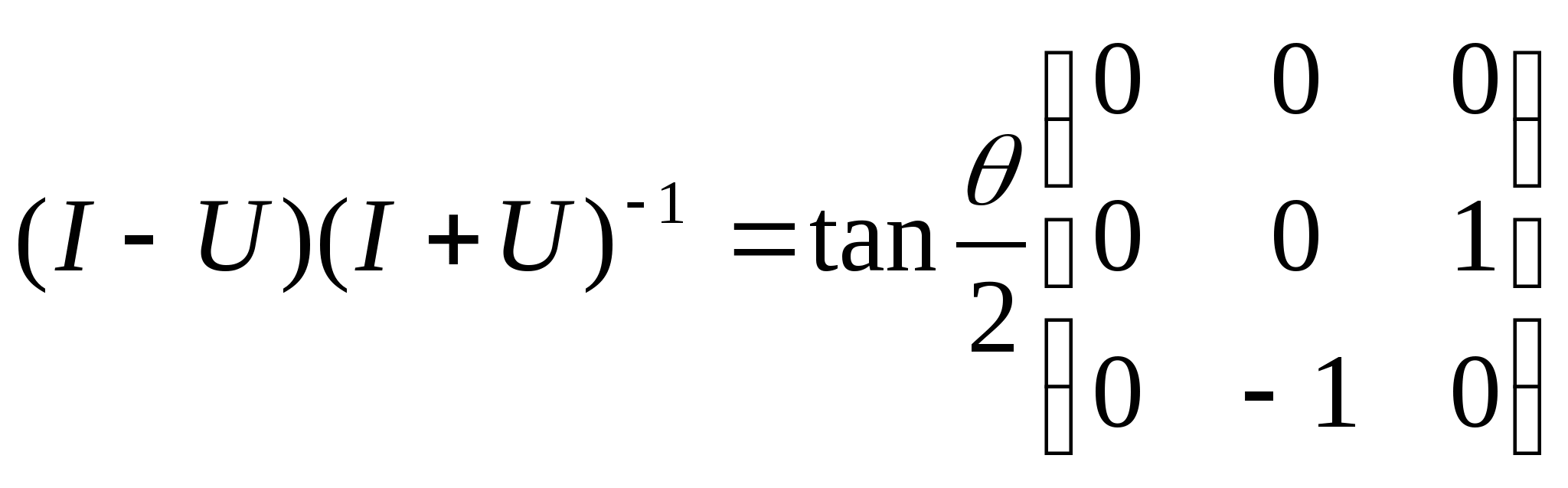
12.证明:如果一个上三角形矩阵
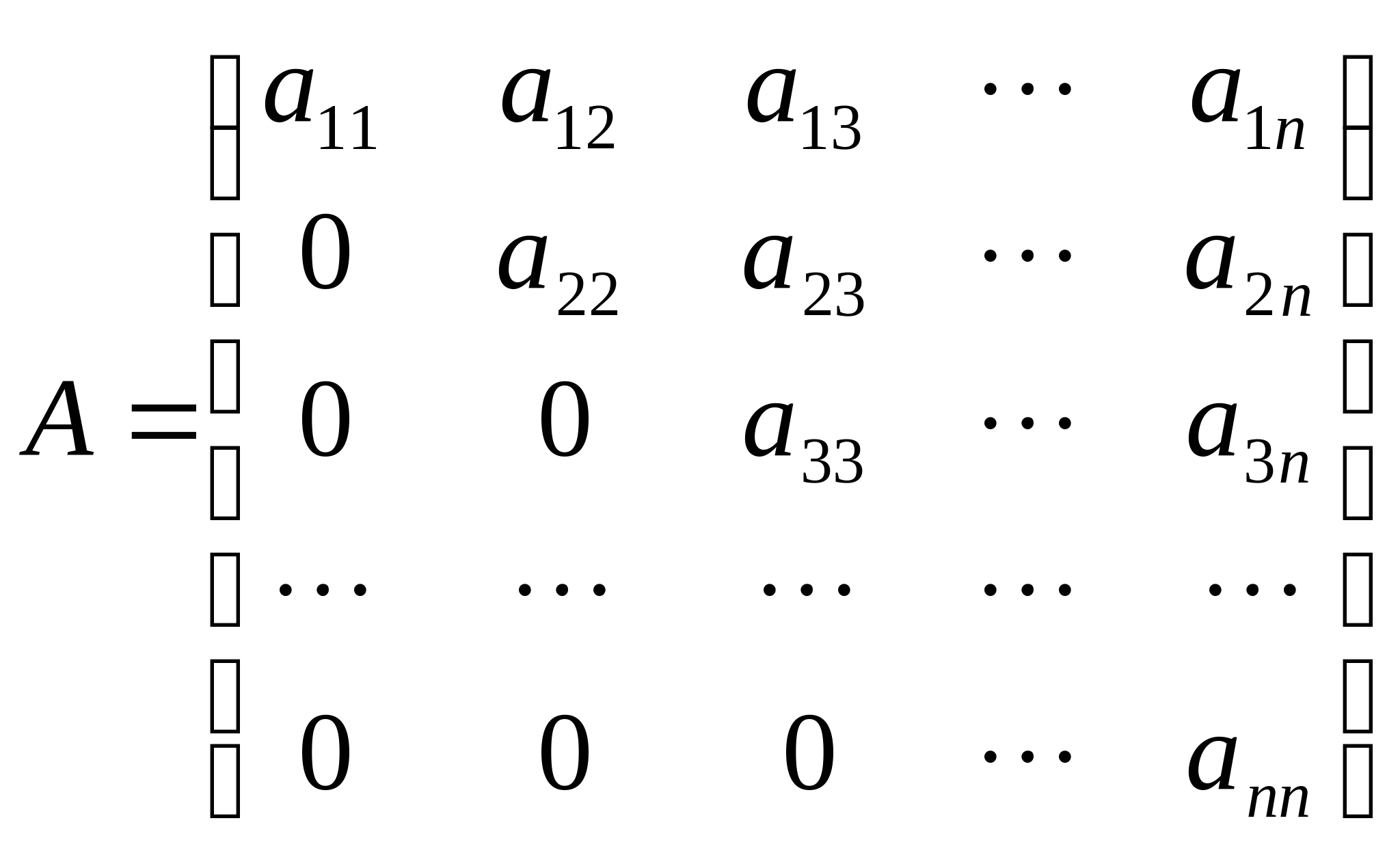
是正交矩阵,那么A一定是对角形矩阵,且主对角线上元素![]() 是1或-1.
是1或-1.
§8.3正交变换
1.证明:![]() 维欧氏空间的两个正交变换的乘积是一个正交变换;一个正交变换的逆变换还是一个正交变换.
维欧氏空间的两个正交变换的乘积是一个正交变换;一个正交变换的逆变换还是一个正交变换.
2.设![]() 是
是![]() 维欧氏空间V的一个正交变换.证明:如果V的一个子空间W在
维欧氏空间V的一个正交变换.证明:如果V的一个子空间W在![]() 之下不变,那么W的正交补
之下不变,那么W的正交补![]() 也在
也在![]() 下不变.
下不变.
3.设V是一个欧氏空间,![]()
![]() 是一个非零向量.对于
是一个非零向量.对于![]() ,规定
,规定
![]() .
.
证明,![]() 是V的一个正交变换,且
是V的一个正交变换,且![]() ,
,![]() 是单位变换.
是单位变换.
线性变换![]() 叫做由向量
叫做由向量![]() 所决定的一个镜面反射.当V是一个
所决定的一个镜面反射.当V是一个![]() 维欧氏空间时,证明,存在V的一个标准正交基,使得
维欧氏空间时,证明,存在V的一个标准正交基,使得![]() 关于这个基的矩阵有形状:
关于这个基的矩阵有形状:
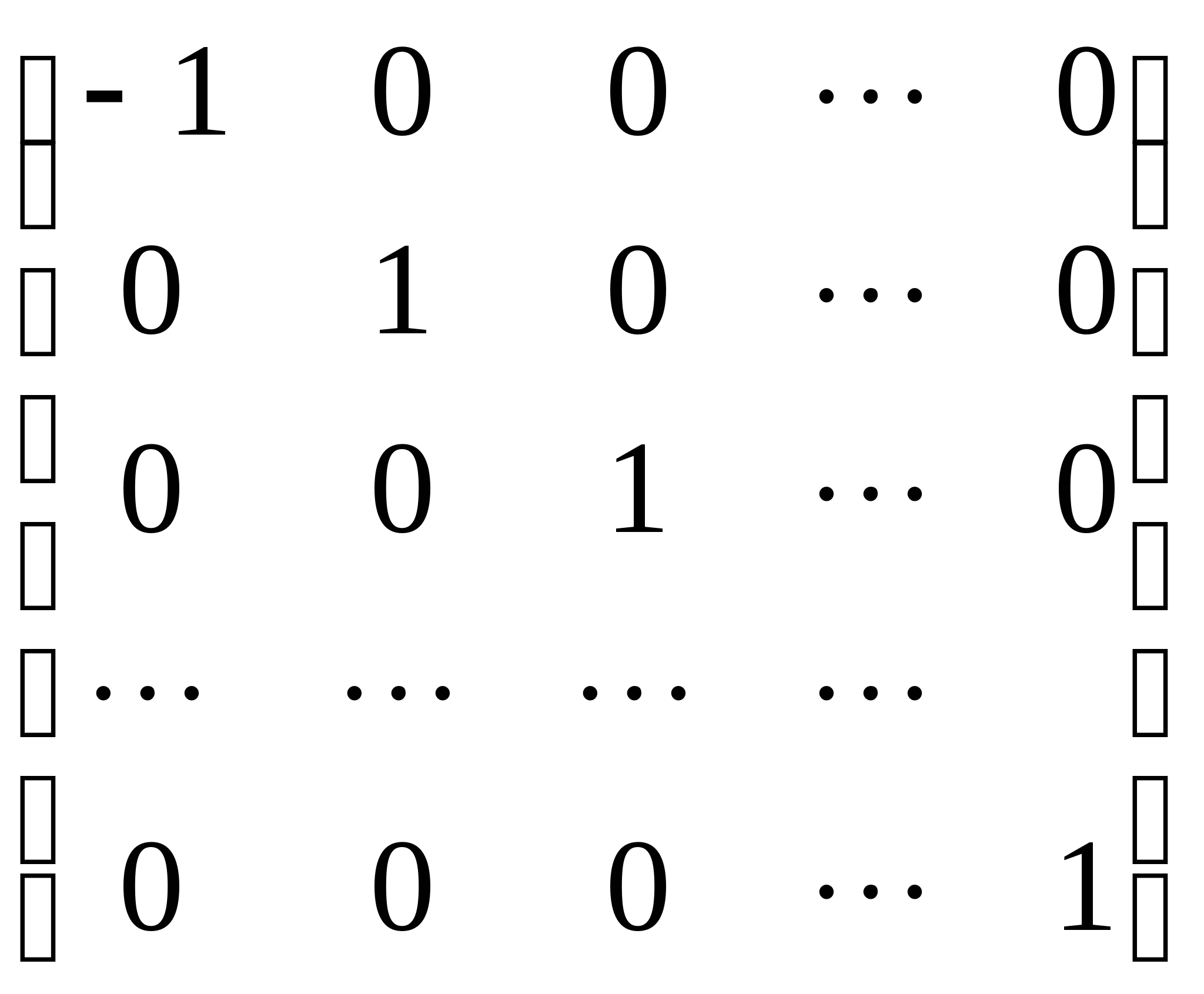
在三维欧氏空间里说明线性变换![]() 的几何意义.
的几何意义.
4.设![]() 是欧氏空间V到自身的一个映射,对
是欧氏空间V到自身的一个映射,对![]() 有
有![]() 证明
证明![]() 是V的一个线性变换,因而是一个正交变换.
是V的一个线性变换,因而是一个正交变换.
5.设U是一个三阶正交矩阵,且![]() .证明:
.证明:
![]() U有一个特征根等于1;
U有一个特征根等于1;
![]() U的特征多项式有形状
U的特征多项式有形状
![]()
这里![]() .
.
6.设![]() 和
和![]() 是
是![]() 维欧氏空间V的两个规范正交基.
维欧氏空间V的两个规范正交基.
![]() 证明:存在V的一个正交变换
证明:存在V的一个正交变换![]() ,使
,使![]() .
.
![]() 如果V的一个正交变换
如果V的一个正交变换![]() 使得
使得![]() ,那么
,那么![]() 所生成的子空间与由
所生成的子空间与由![]() 所生成的子空间重合.
所生成的子空间重合.
7.令V是一个![]() 维欧氏空间.证明:
维欧氏空间.证明:
![]() 对V中任意两不同单位向量
对V中任意两不同单位向量![]() ,存在一个镜面反射
,存在一个镜面反射![]() ,使得
,使得![]() .
.
![]() V中每一正交变换
V中每一正交变换![]() 都可以表成若干个镜面反射的乘积.
都可以表成若干个镜面反射的乘积.
[提示:为了证明![]() ,利用
,利用![]() 和习题6.]
和习题6.]
8.证明:每一个![]() 阶非奇异实矩阵A都可以唯一地表示成
阶非奇异实矩阵A都可以唯一地表示成
![]()
的形式,这里![]() 是一个正交矩阵,
是一个正交矩阵,![]() 是一个上三角形实矩阵,且主对角线上元素都是正数.
是一个上三角形实矩阵,且主对角线上元素都是正数.
[提示:非奇异矩阵A的列向量![]() 作成
作成![]() 维列空间
维列空间![]() 的一个基.对这个基施行正交化,得出
的一个基.对这个基施行正交化,得出![]() 的一个规范正交基
的一个规范正交基![]() ,以这个规范正交基为列的矩阵U是一个正交矩阵,写出
,以这个规范正交基为列的矩阵U是一个正交矩阵,写出![]() 由
由![]() 的表示式,就可以得出矩阵T.证明唯一性时,注意8.2习题12.]
的表示式,就可以得出矩阵T.证明唯一性时,注意8.2习题12.]
§8.4 对称变换和对称矩阵
1.设![]() 是
是![]() 维欧氏空间V的一个线性变换.证明,如果
维欧氏空间V的一个线性变换.证明,如果![]() 满足下列三个条件的任意两个,那么它必然满足第三个:
满足下列三个条件的任意两个,那么它必然满足第三个:![]()
![]() 是正交变换;
是正交变换;![]()
![]() 是对称变换;
是对称变换;![]()
![]() 是单位变换.
是单位变换.
2.设![]() 是
是![]() 维欧氏空间V的一个对称变换,且
维欧氏空间V的一个对称变换,且![]() .证明,存在V的一个规范正交基,使得
.证明,存在V的一个规范正交基,使得![]() 关于这个基的矩阵有形状
关于这个基的矩阵有形状

3.证明:两个对称变换的和还是一个对称变换.两个对称变换的乘积是不是对称变换?找出两个对称变换的乘积是对称变换的一个充要条件.
4.![]() 维欧氏空间V的一个线性变换
维欧氏空间V的一个线性变换![]() 说是斜对称的,如果对于任意向量
说是斜对称的,如果对于任意向量![]() ,
,
![]() .
.
证明:
![]() 斜对称变换关于V的任意规范正交基的矩阵都是斜对称的实矩阵(满足条件
斜对称变换关于V的任意规范正交基的矩阵都是斜对称的实矩阵(满足条件![]() 的矩阵叫做斜对称矩阵)
的矩阵叫做斜对称矩阵)
![]() 反之,如果线性变换
反之,如果线性变换![]() 关于V的某一规范正交基的矩阵是斜对称的,那么
关于V的某一规范正交基的矩阵是斜对称的,那么![]() 一定是斜对称线性变换.
一定是斜对称线性变换.
![]() 斜对称实矩阵的特征根或者是零,或者是纯虚数.
斜对称实矩阵的特征根或者是零,或者是纯虚数.
5.令A是一个斜对称实矩阵.证明,![]() 可逆,并且
可逆,并且![]() 是一个正交矩阵.
是一个正交矩阵.
6.对于下列对称矩阵A,各求出一个正交矩阵U,使得![]() 是对角形式:
是对角形式:
![]()
 ;
; ![]()