第二章 多项式
日期:
阅读次数:
2018-03-15
285
第二章 多项式
1.证明:多项式![]() 能整除
能整除![]() .的充分与必要条件是
.的充分与必要条件是![]() 为偶数.
为偶数.
2.设![]() 为大于1的整数.证明:当且仅当
为大于1的整数.证明:当且仅当![]() 和
和![]() 互素时多项式
互素时多项式
![]() 与
与![]() 互素.
互素.
3.设![]() 是一个次数大于零的多项式.证明:
是一个次数大于零的多项式.证明:![]() 是某个不可约多项式方幂的充分与必要条件是,对任意多项式
是某个不可约多项式方幂的充分与必要条件是,对任意多项式![]() 和
和![]() ,由
,由![]() 可推出
可推出![]() ,或有某正整数
,或有某正整数![]() ,使
,使![]() .
.
4.设![]() 为有理系数多项式
为有理系数多项式![]() 的一个
的一个![]() 重根,证明:若
重根,证明:若![]() 为有理数,
为有理数,![]() 为正有理数且
为正有理数且![]() 为无理数,则
为无理数,则![]() 也是
也是![]() 的一个
的一个![]() 重根.
重根.
5.设![]() 是整系数多项式,证明:如果
是整系数多项式,证明:如果![]() 是奇数,则
是奇数,则![]() 在有理数域上不可约.
在有理数域上不可约.
6.证明:次数>0且首项系数为1的多项式![]() 是某一个不可约多项式的方幂的充分要条件是,对任意的多项式
是某一个不可约多项式的方幂的充分要条件是,对任意的多项式![]() ,
,![]() ,由
,由![]()
![]() 可以推出
可以推出![]() |
|![]() ,或者对某一正整数m,
,或者对某一正整数m,![]() .
.
7.证明:![]() 不能有不为零的重数大于2的根.
不能有不为零的重数大于2的根.
8.证明:如果![]() ,那么
,那么![]() 的根只能是零或单位根.
的根只能是零或单位根.
9.如果![]() ,证明:
,证明:![]() 有n重根,其中n =
有n重根,其中n = ![]() .
.
10.设![]() 是n个不同的数,而
是n个不同的数,而![]() .证明:
.证明:
1)![]() = 1;
= 1;
2)任意多项式![]() 用
用![]() 除所得的余式为
除所得的余式为![]() .
.
11.![]() 与
与![]() 同上题,
同上题,![]() 是任意n个数,显然
是任意n个数,显然![]() 适合条件
适合条件![]() ,
,![]() 。这称为拉格朗日(Lagrange)插值公式。利用上面的公式求:
。这称为拉格朗日(Lagrange)插值公式。利用上面的公式求:
一个次数< 4的多项式
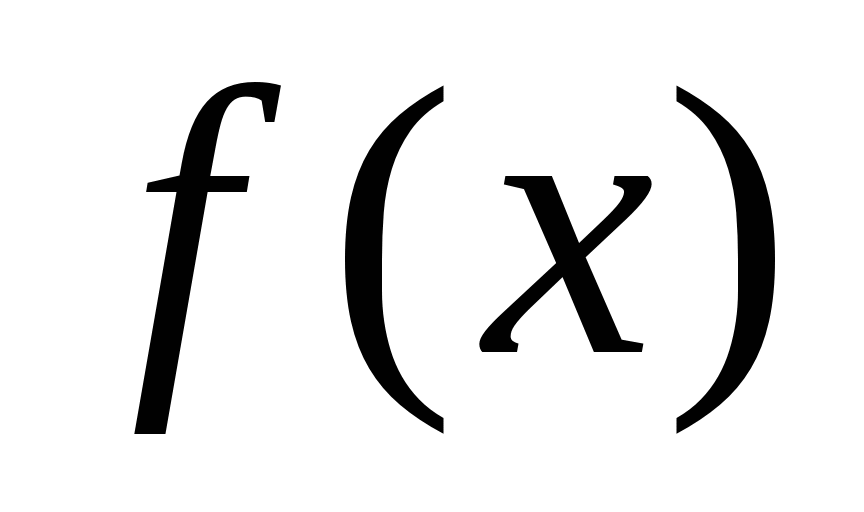 ,它适合条件:
,它适合条件: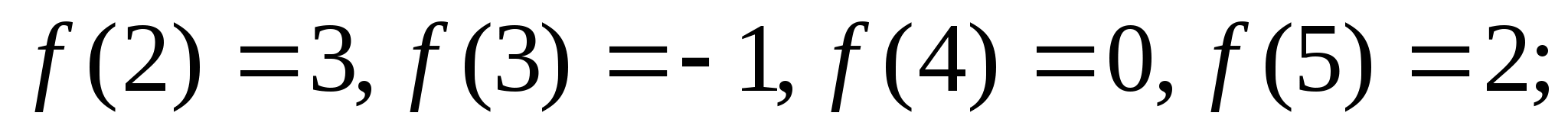
一个二次多项式
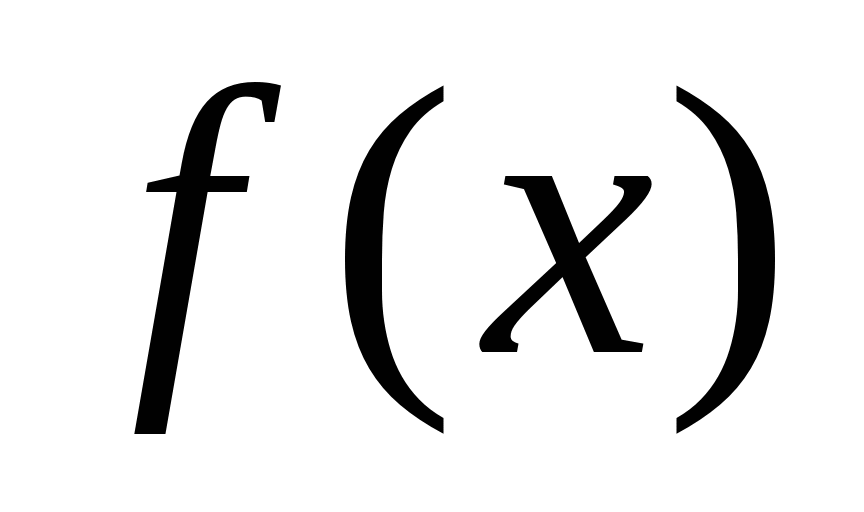 ,它在x = 0,
,它在x = 0,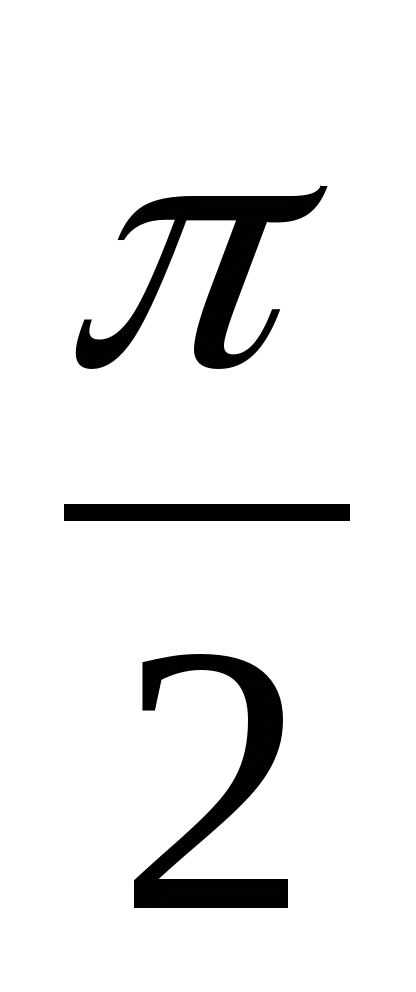 ,
, 处与函数
处与函数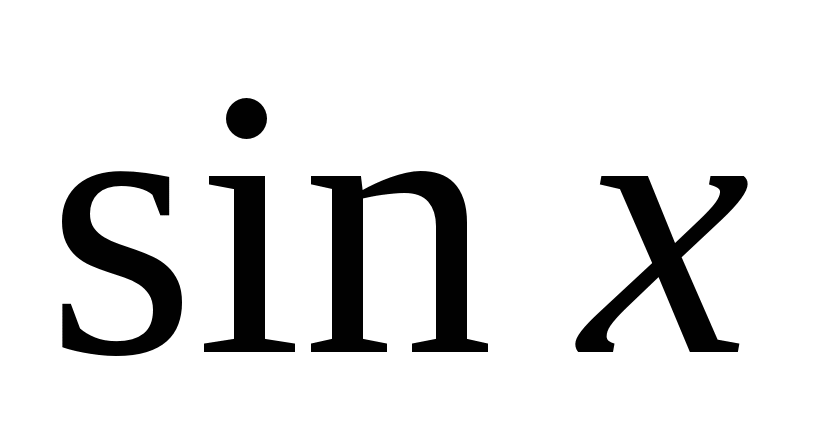 有相同的值;
有相同的值;一个次数尽可能低的多项式
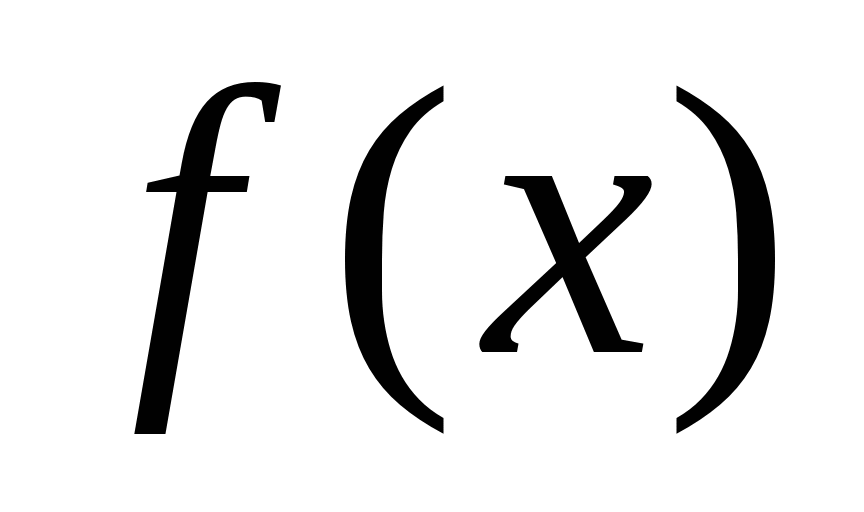 ,使
,使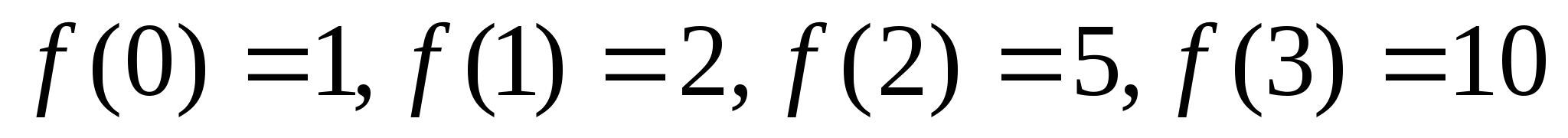 .
.
12.设![]() 是方程
是方程![]() 的根,证明:
的根,证明:![]() 的对称多项式可以表成
的对称多项式可以表成![]() 与
与![]() 的多项式.
的多项式.
13.![]() 。令
。令![]() (
(![]() ).
).
证明:
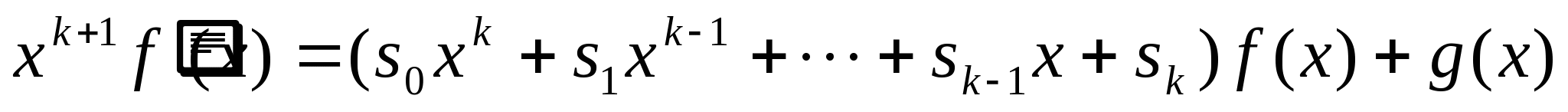 ,其中
,其中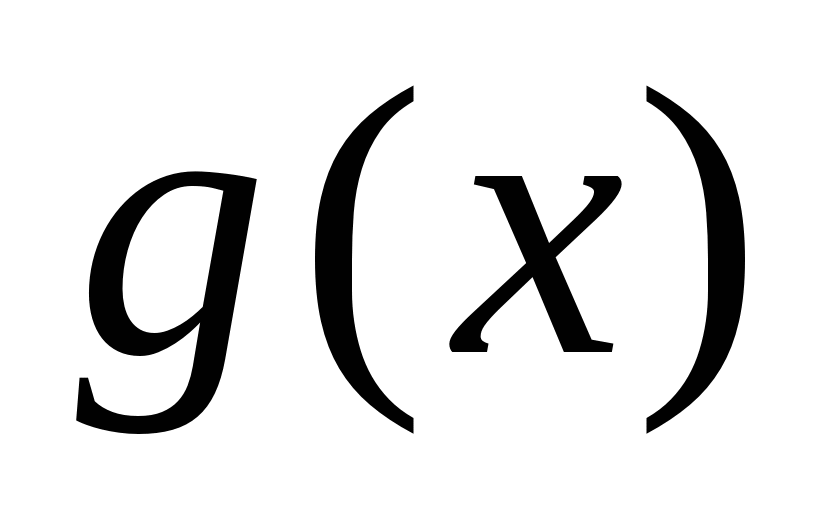 的次数
的次数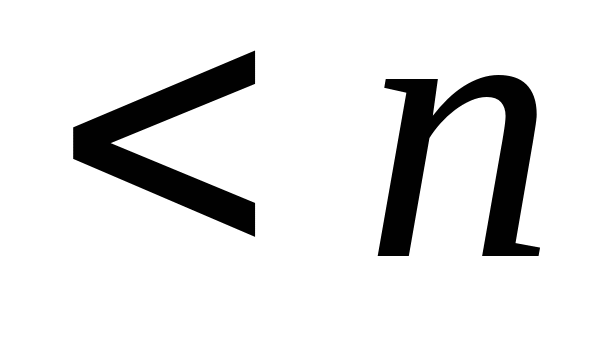 或
或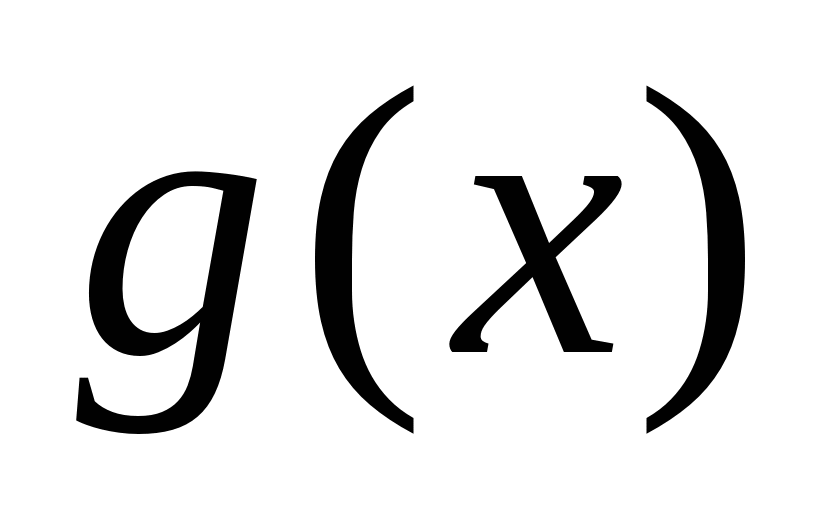 =0.
=0.由上式证明牛顿(Newton)公式:
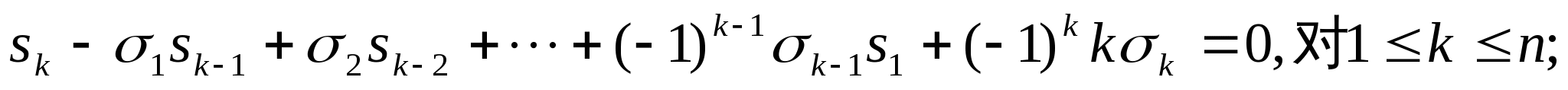
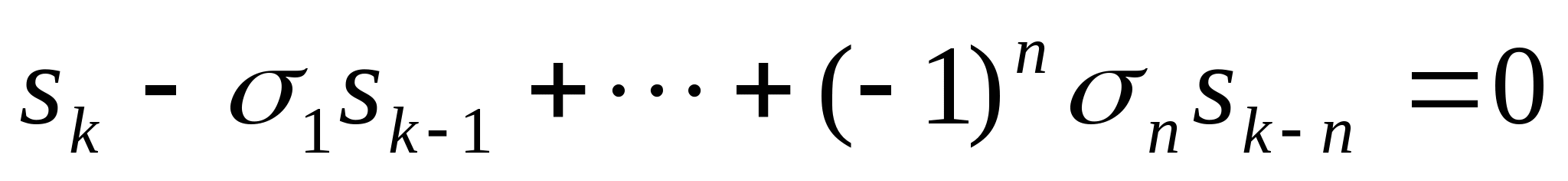 ,对于
,对于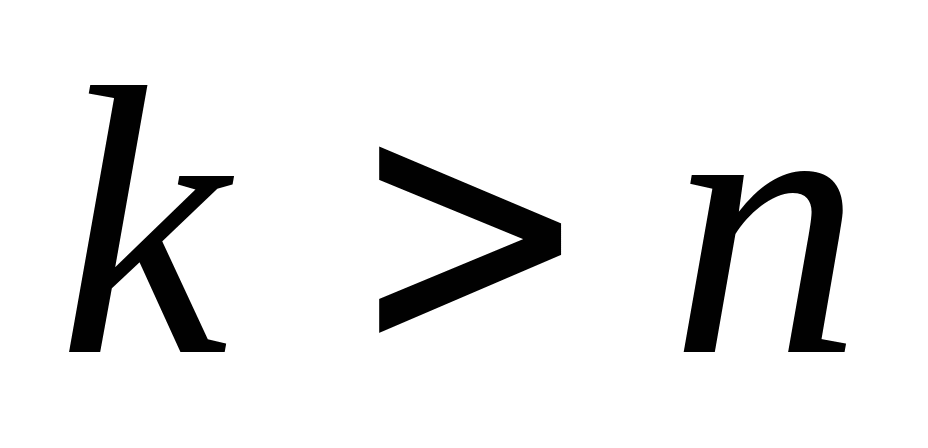 .
.
14.根据牛顿公式用初等对称多项式表示![]() .
.
15.证明:如果对于某一个6次方程有![]() ,那么
,那么![]() ﹒
﹒![]()
![]() .
.
16.求一个n次方程使![]() .
.
17.求一个n次方程使![]() .
.