第四章 线性方程组

1.设D为方程组,①

的系数行列式,为把D中第j列换成常数项所得的行列式.

(1) 证明:此方程组有唯一解的充分必要条件是;

(2) 当时,此方程组必有无穷多解,对不对?

2.证明:如果方程组

         ①

的系数矩阵A与矩阵

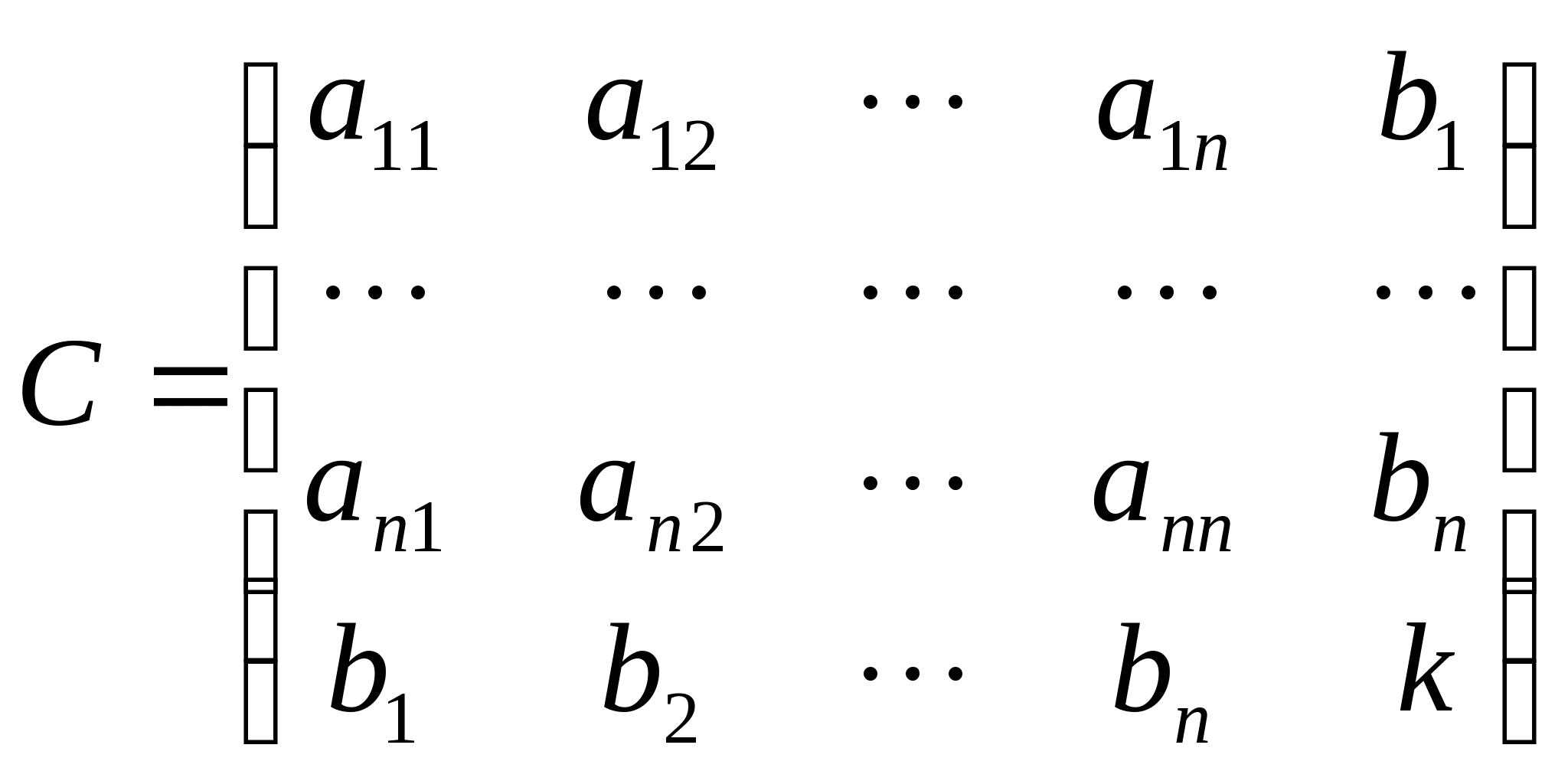
的秩相等,则此方程组有解.

3.解方程组

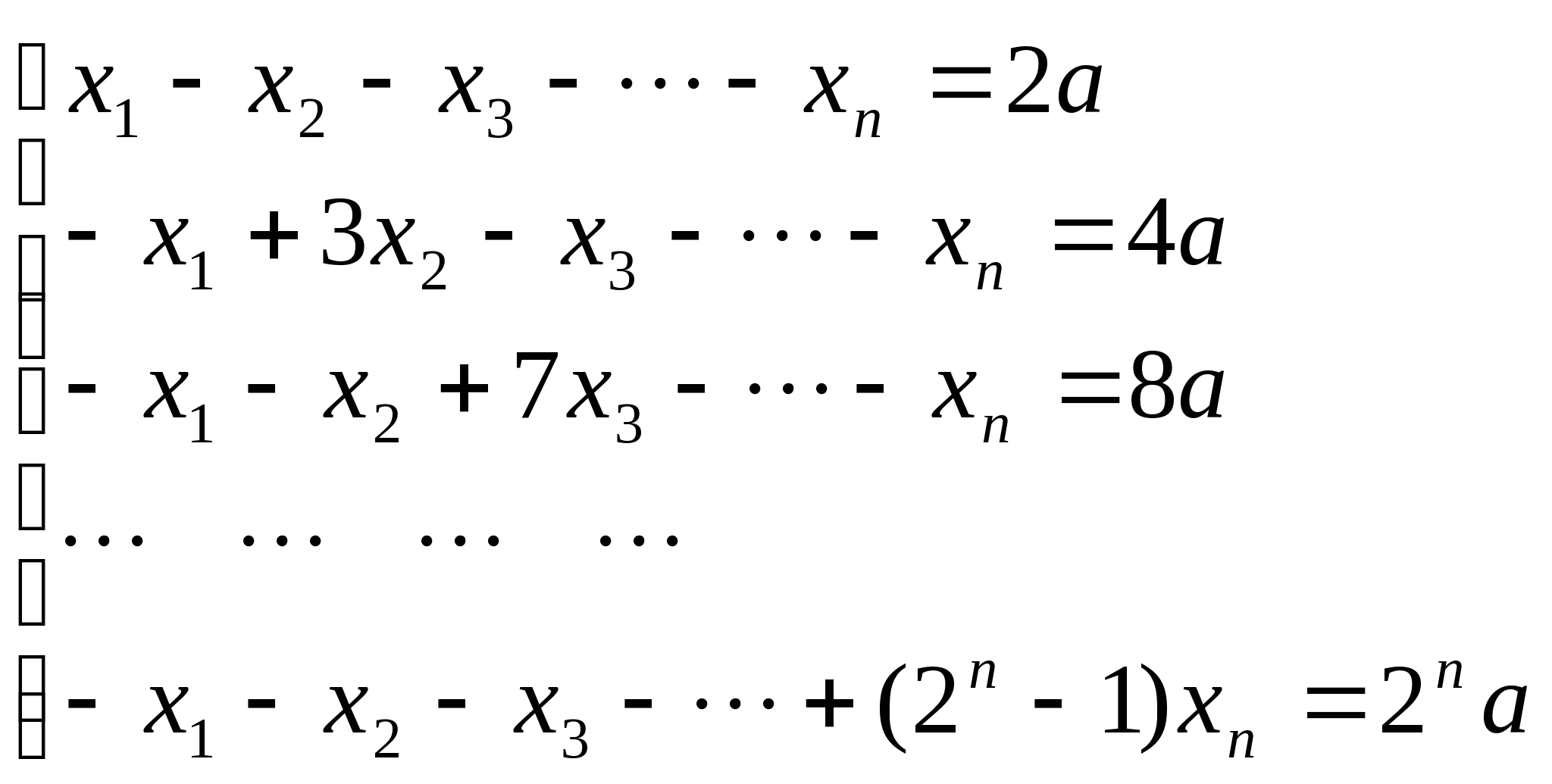
(提示:令)

4．设，均为实数，证明：性线性方程组必有解．

5．证明：方程有解的充分必要条件是从一定能推出．

6．设有阶矩阵，若满足，则．