第九章  二次型

1.设A,B是阶对称矩阵,B是非奇异的.又设的根互异,分别是齐次线性方程组的非零解,证明:

的线性无关.

2.设A,B,C为阶方阵,且正定,证明:也是正定的.

3.用非退化线性替换化下列二次型为标准形，并用矩阵验算所得结果：

(1) ；

(2) ；

(3) +；

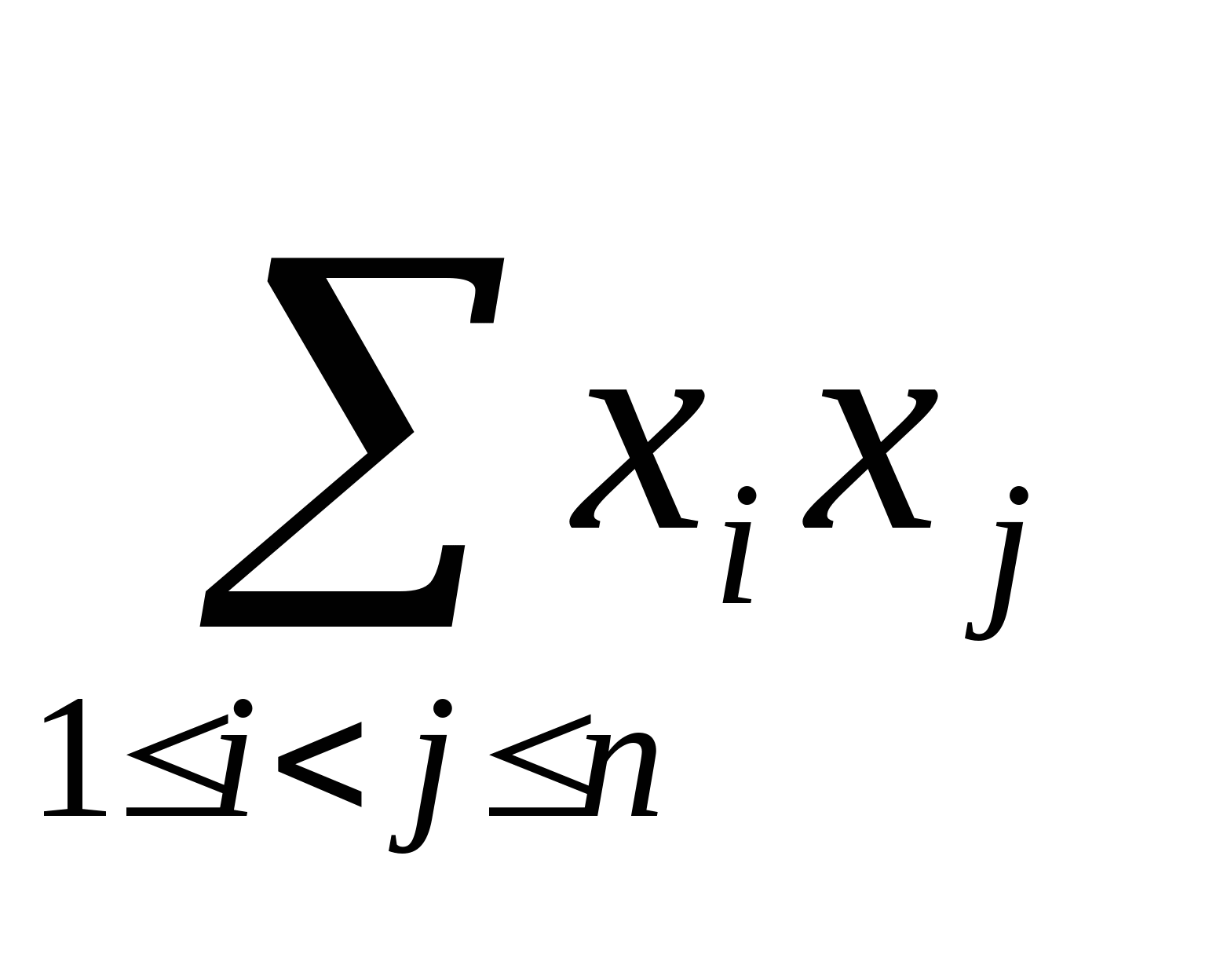(4) ，其中．

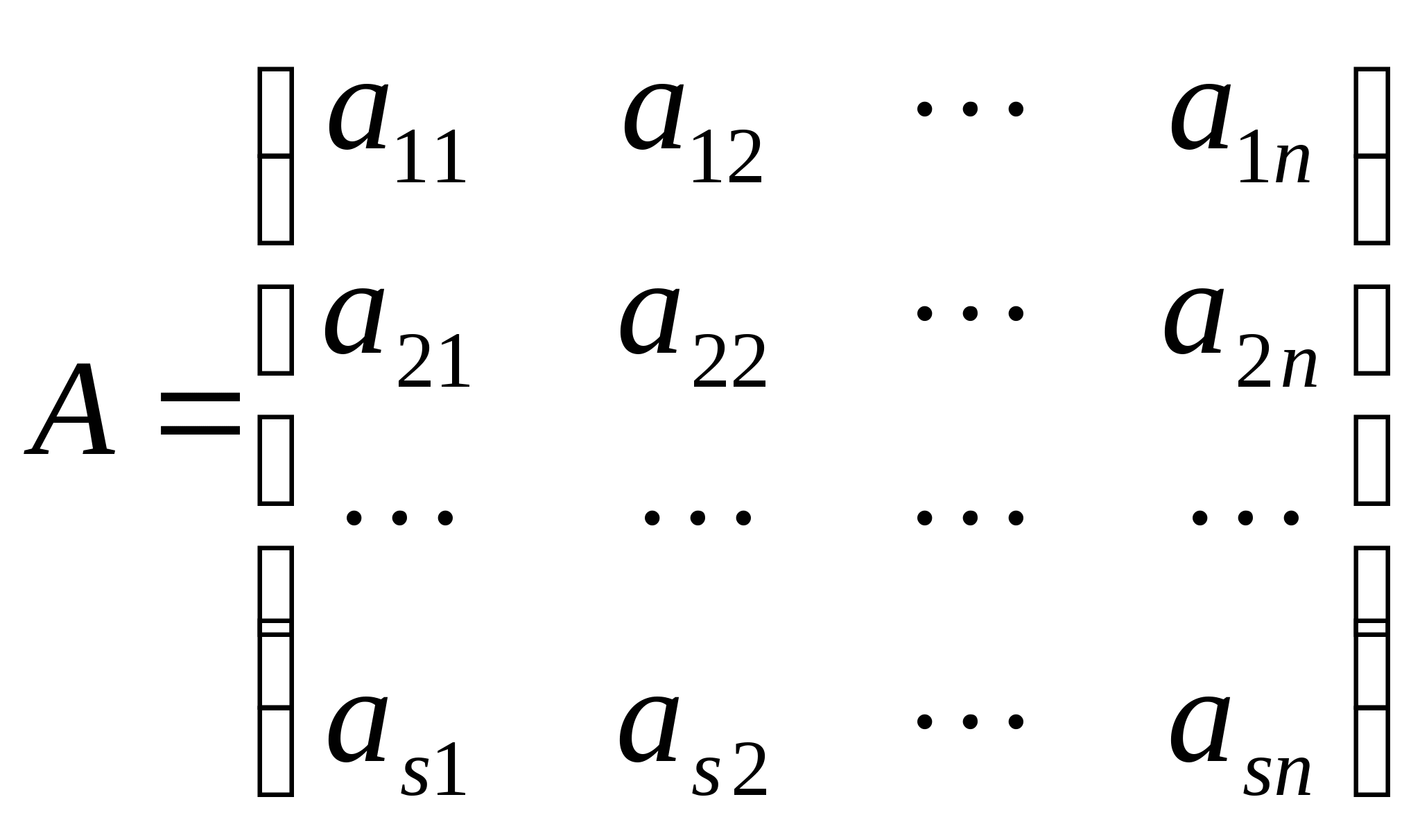4.设实二次型=，证明：的秩等于矩阵的秩．

5．设A是n阶实对称矩阵，证明：存在一正实数c使对任一个实n维向量X都有.

6．证明:

(1) 如果是正定二次型，那么

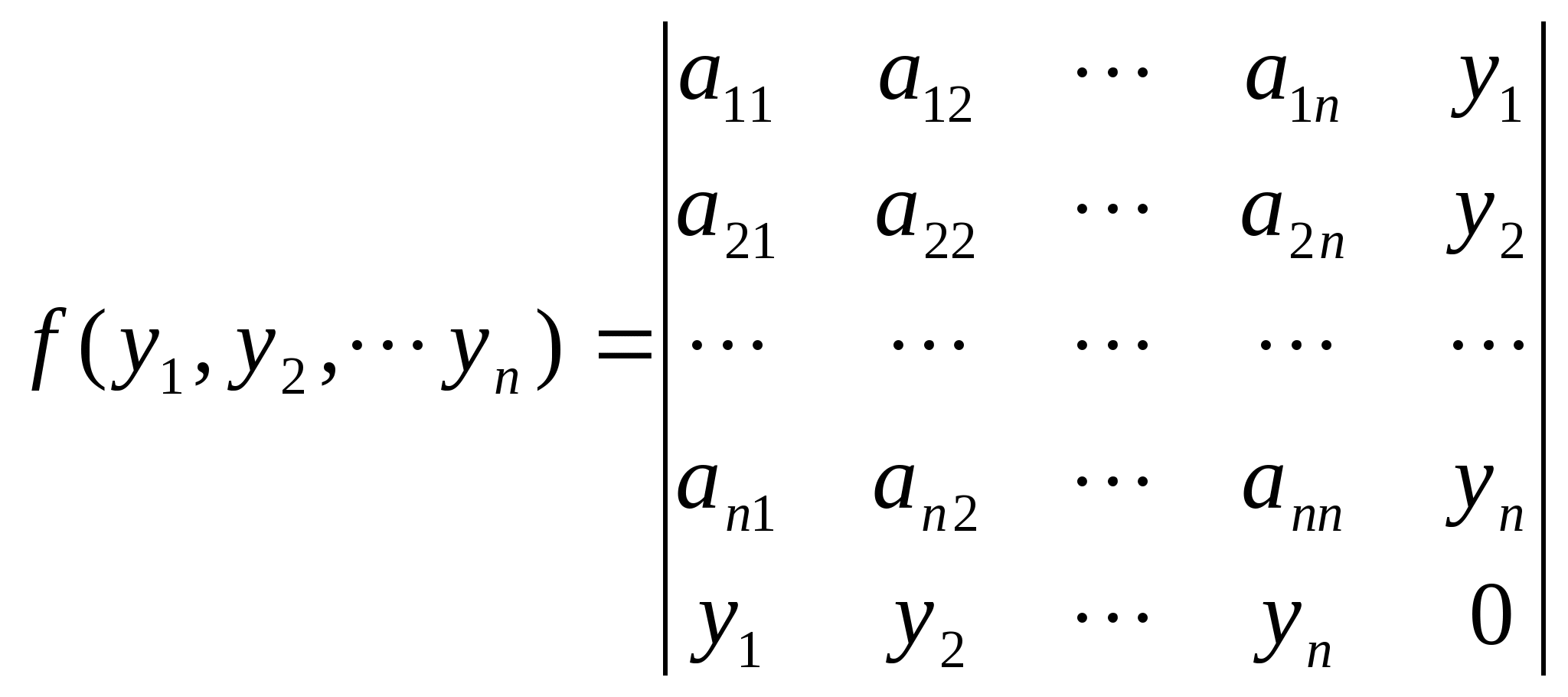
 是负定二次型；

(2)如果A是正定矩阵，那么，这里是A的阶的顺序主子式．

(3)如果A是正定矩阵，那么.

(4)如果是阶实对称矩阵,那么

．

7．证明：实对称矩阵A是半正定的充分必要条件是A的一切主子式全大于或等于零（所谓k阶主子式是指形为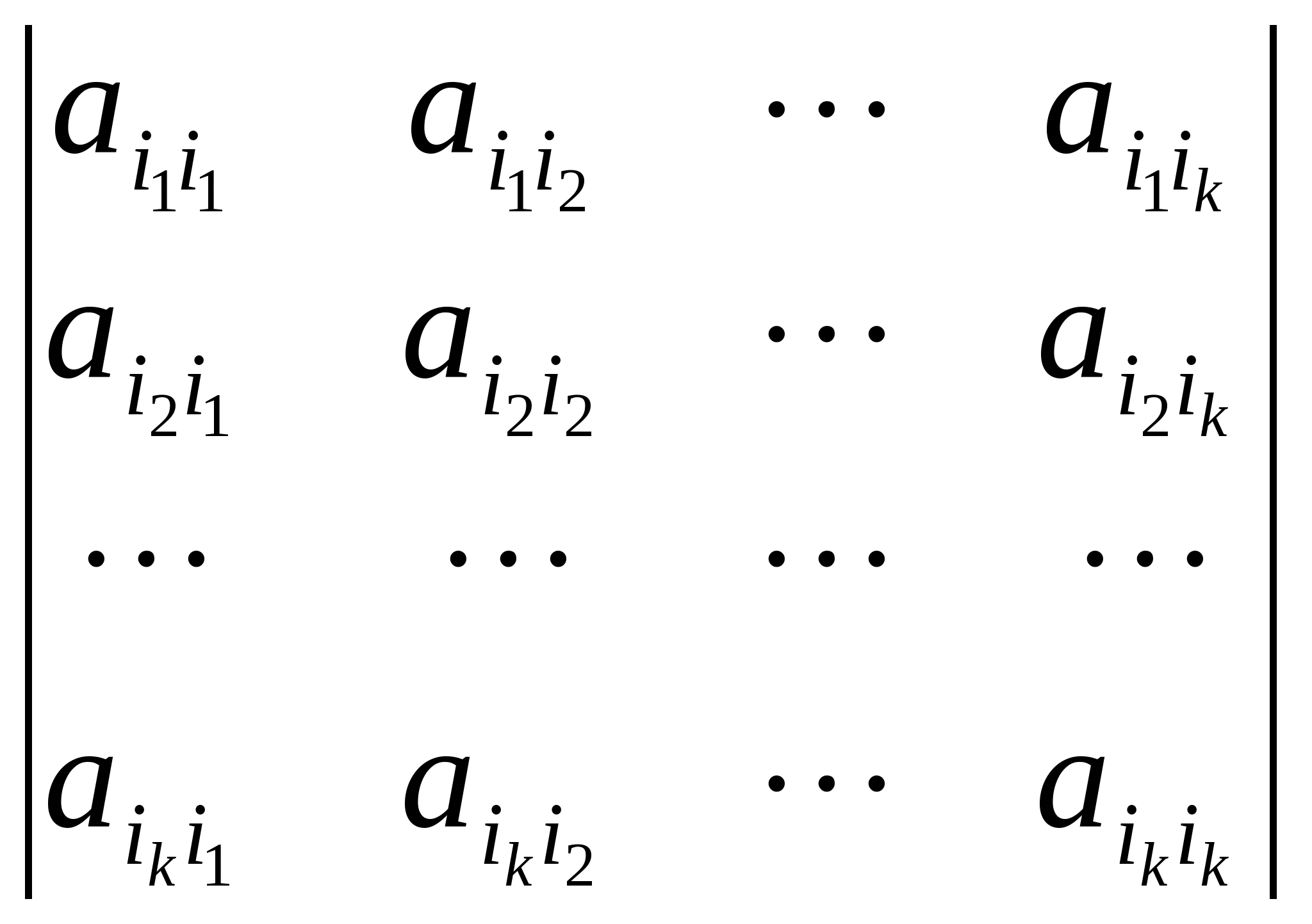的k阶子式，其中）