第四章  线性方程组

自测题

一、填空题（每小题3分，共15分）   

1．线性方程组无解，且则

2．若方程组有无穷多解，则

3．设A是方阵，线性方程组有非零解的充分必要条件是

4．当时，的秩为

5．设且A经若干次第三种初等变换化为，则

二、判断说明题（先判断正确与错误，再简述理由。每小题5分，共20分）

1．齐次线性方程组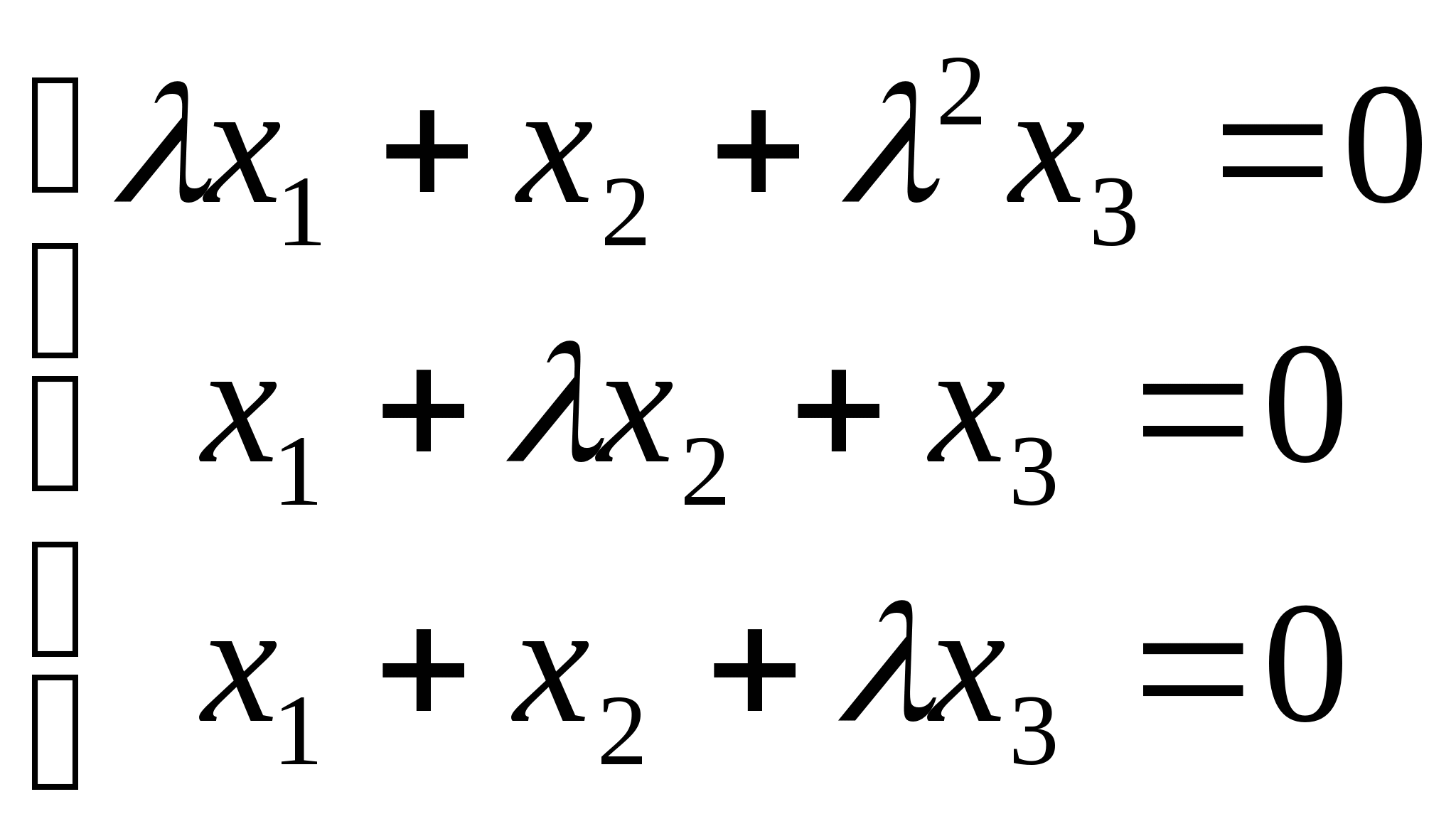的系数矩阵为A，若存在三阶矩阵使得则且

2．非齐次线性方程组有解，若其解不唯一，则必有无穷多个解．

3．设A是n阶方阵，是有无穷多解的充分必要条件．

4．若齐次线性方程组中方程的个数小于未知量的个数，则方程组必有无穷多解．

三. 计算题（每小题15分，共45分）

1．取何值时，方程组有唯一解？有无穷多解？无解？

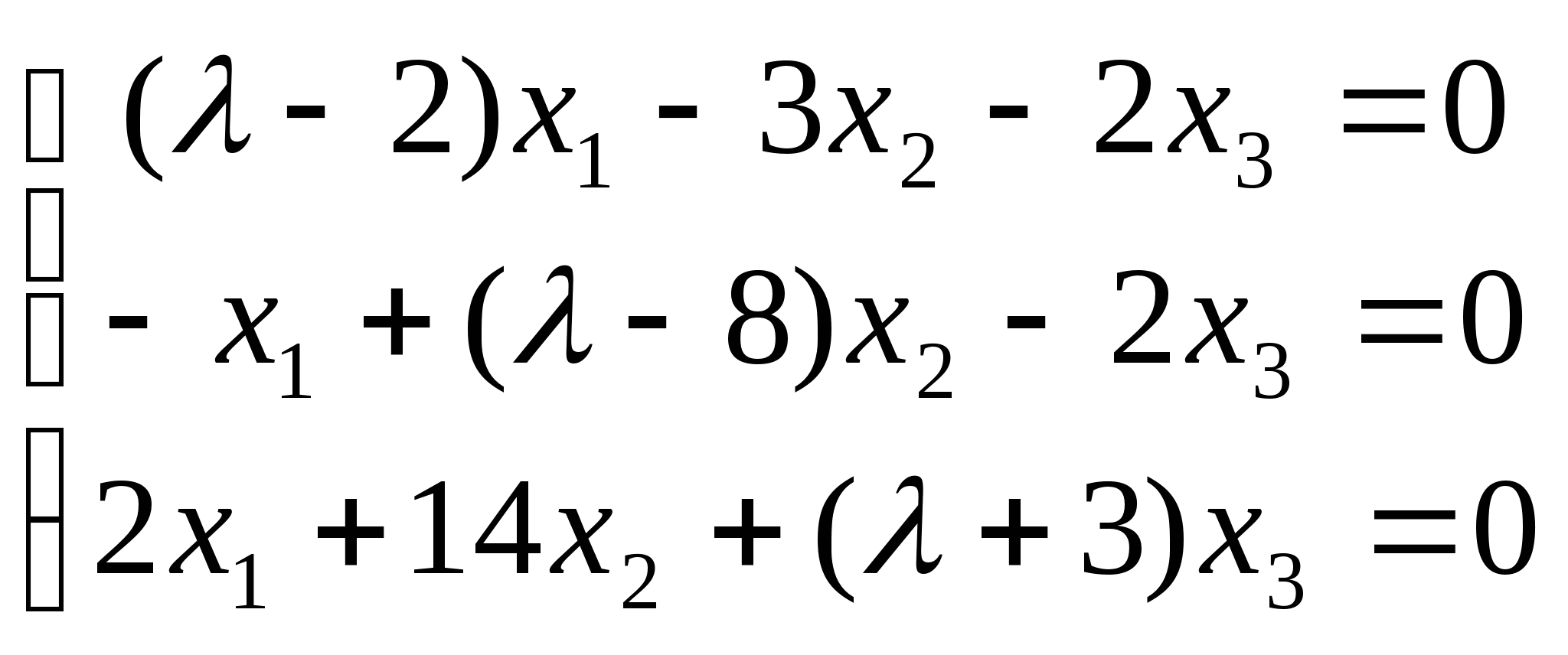2．取何值时，齐次线性方程组有非零解？并求出一般解.

3．给定两个线性方程组：

求的通解

取何值时，与同解？

四、证明题（每小题10分，共20分）

1．设方程组

证明此方程组对任意实数都有解，并且求它的一切解.

2．设线性方程组

的系数矩阵A的秩等于矩阵

B=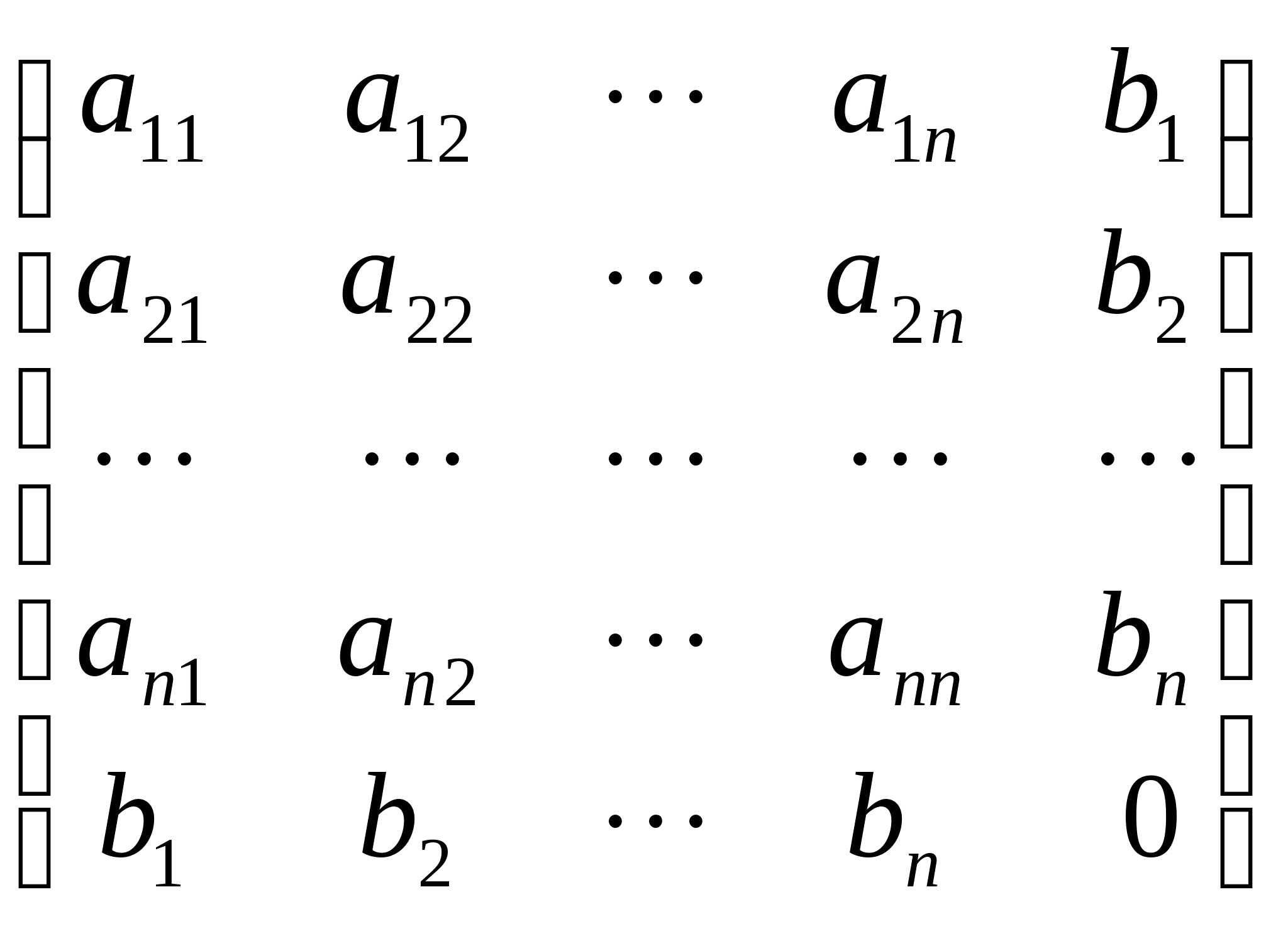

的秩，证明方程组（*）有解.问：逆命题是否成立？为什么？