第七章 线性变换
日期:
阅读次数:
2018-03-15
119
第七章 线性变换
自测题
一、填空题(每小题3分,共18分)
1.![]() 是
是![]() 上的线性变换,若
上的线性变换,若![]() ,则
,则![]() .
.
2.![]() :
:![]() ,
,![]() ;
;![]() :
:![]() ,
,![]() ,则
,则![]() .
.![]() .
.![]() .
.
3.设![]() ,则向量
,则向量![]() 是A的属于特征值 的特征向量.
是A的属于特征值 的特征向量.
4.若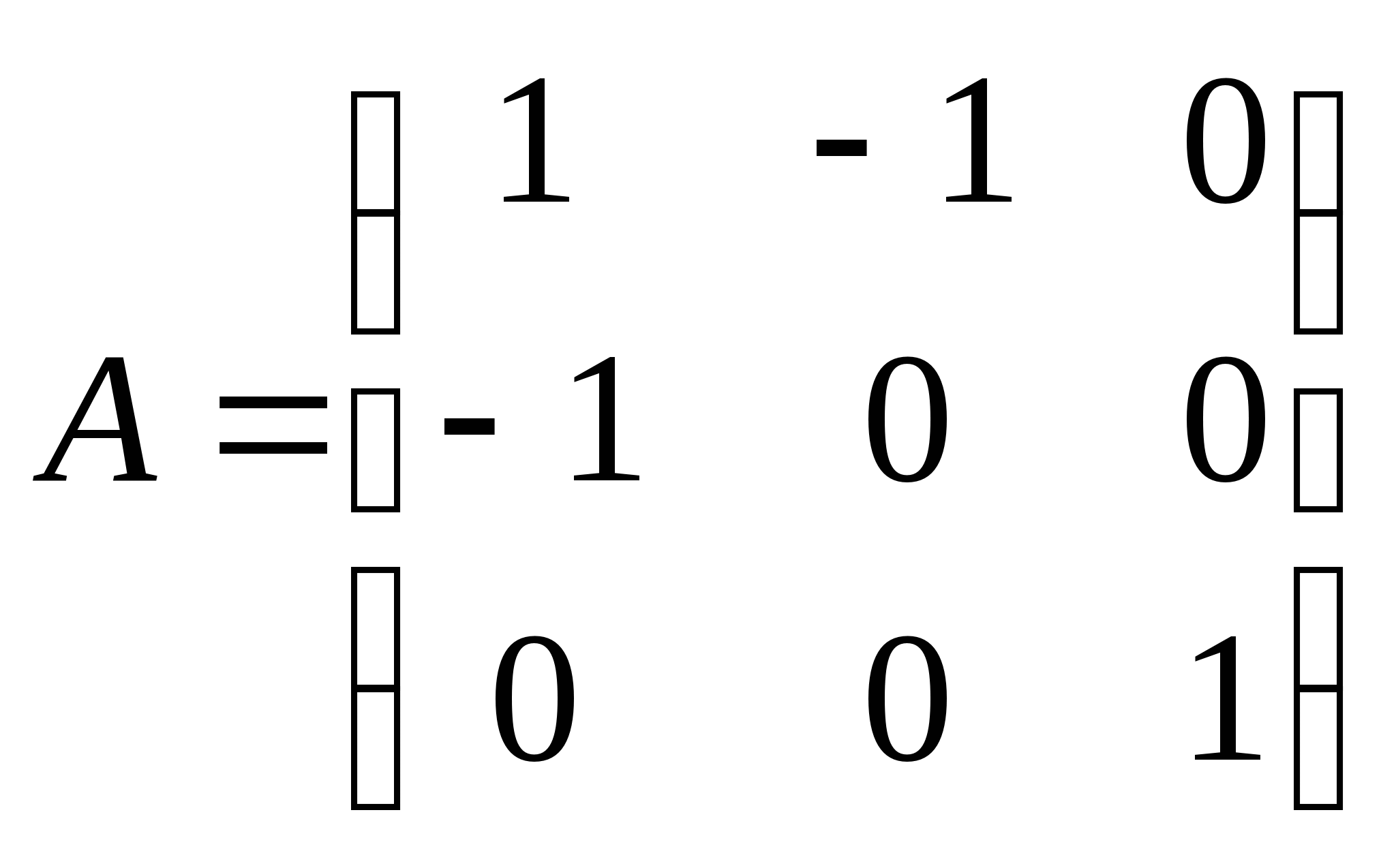 与
与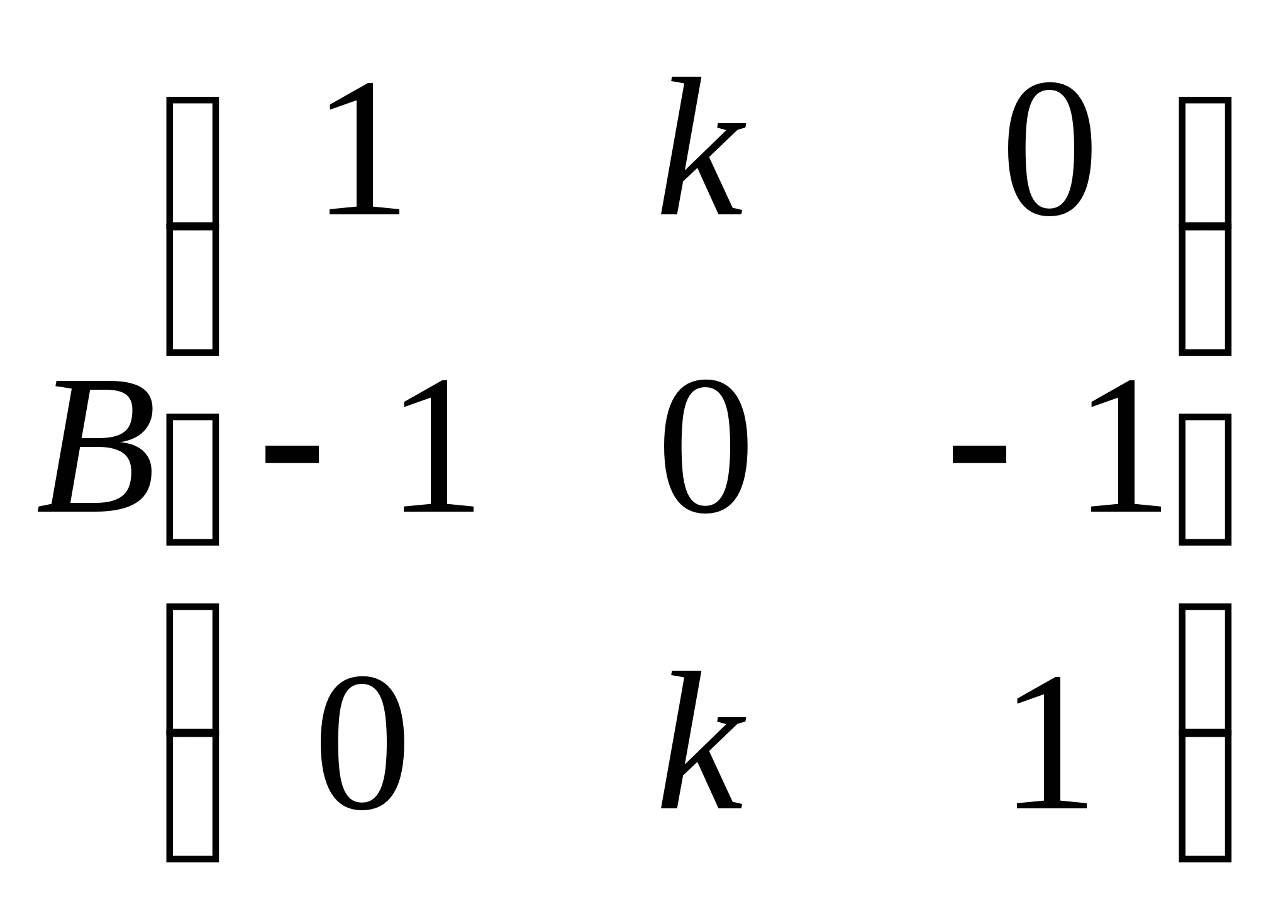 相似,则
相似,则![]() =.
=.
5.设三阶方阵A的特征多项式为![]() ,则
,则![]() .
.
6.![]() 阶方阵A满足
阶方阵A满足![]() ,则
,则![]() 的特征值为.
的特征值为.
二、判断说明题(每小题5分,共20分)
1.![]() 阶方阵A至少有一特征值为零的充分必要条件是
阶方阵A至少有一特征值为零的充分必要条件是![]() .
.
2.已知![]() ,其中
,其中![]() 为
为![]() 阶可逆矩阵,
阶可逆矩阵,![]() 为一个对角矩阵.则A的特征向量与P有关.
为一个对角矩阵.则A的特征向量与P有关.
3.![]() 为V上线性变换,
为V上线性变换,![]() 为V的基,则
为V的基,则![]() 线性无关.
线性无关.
4.![]() 为V上的非零向量,
为V上的非零向量,![]() 为V上的线性变换,则
为V上的线性变换,则![]() 是V的子空间.
是V的子空间.
三、计算题(每小题14分,共42分)
1.设 与
与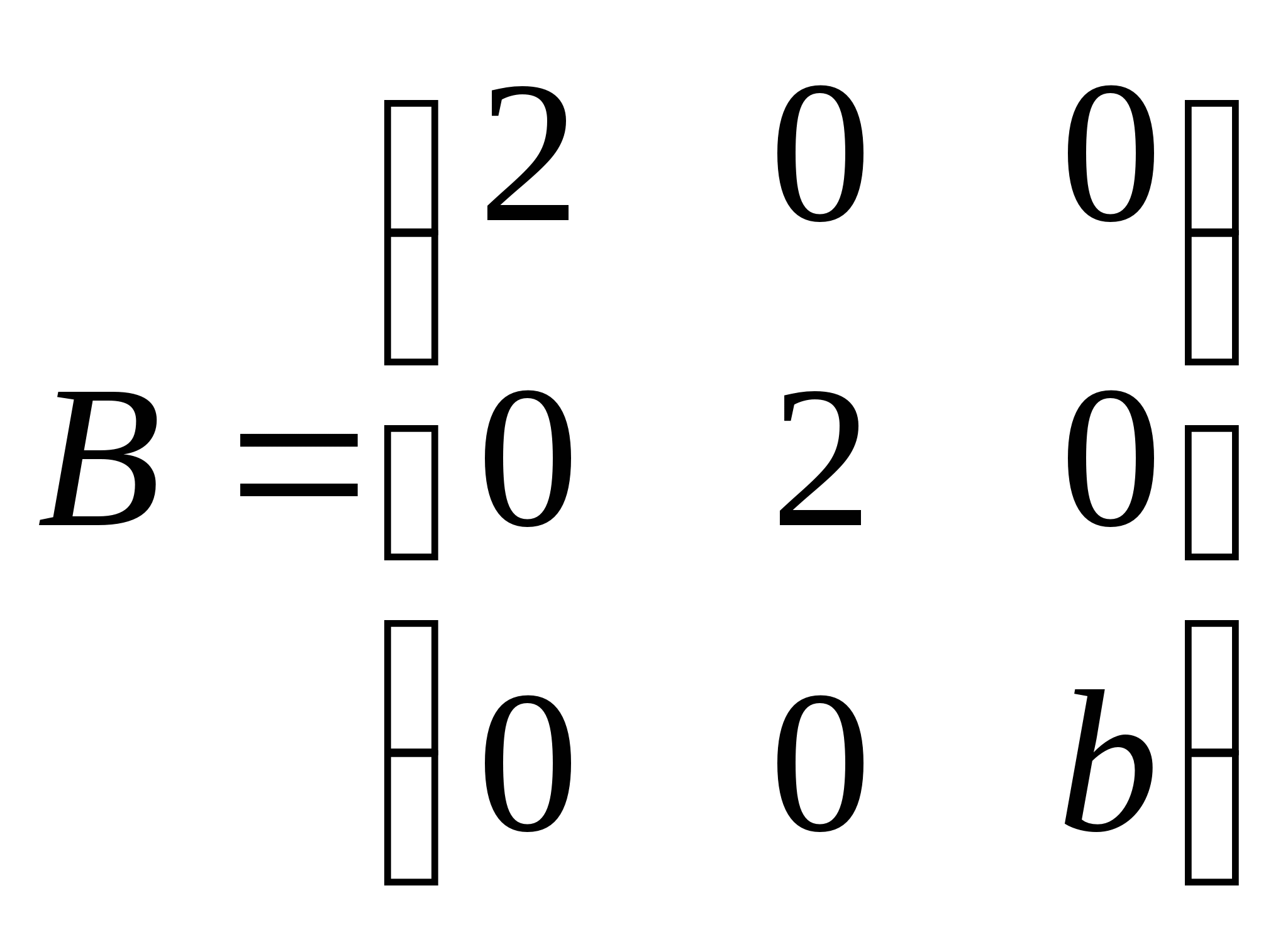 相似.
相似.
(1)求![]() 的值;
的值;
(2)求可逆矩阵,使![]() .
.
2.![]() 中,线性变换
中,线性变换![]() 关于基
关于基![]() ,
,![]() ,
,![]() 的矩阵为
的矩阵为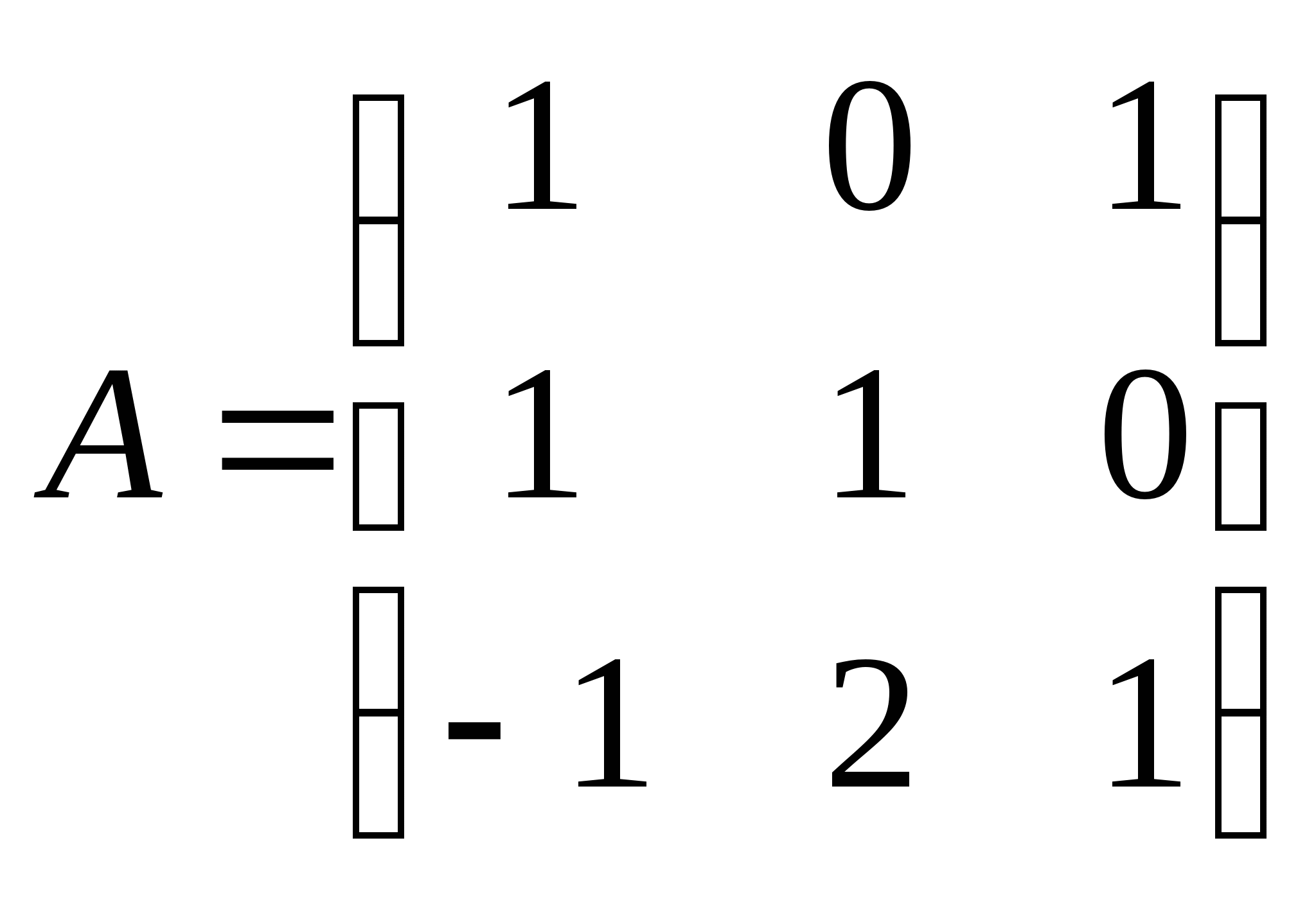
(1)求![]() 关于标准基
关于标准基![]() 的矩阵;
的矩阵;
(2)设![]() ,
,![]() ,求
,求![]() 关于基
关于基![]() 的坐标.
的坐标.
3.设![]() 是
是![]() 的线性变换,
的线性变换,![]()
(1)求![]() 的一个基和维数;
的一个基和维数;
(2)求![]() 的一个基和维数.
的一个基和维数.
四、证明题(每小题10分,共20分)
1.设A是![]() 阶矩阵,且有
阶矩阵,且有![]() ,
,![]() ,证明:-1是A的特征值.
,证明:-1是A的特征值.
2.设![]() 是V上的两个线性变换,证明:
是V上的两个线性变换,证明:
(1)![]() 的充要条件是
的充要条件是![]() ;
;
(2)![]() 的充要条件是
的充要条件是![]() .
.